|
Photo by Cheresa D. Theiral, courtesy U.S. Army. |
Suppose that a rope bridge is constructed using a massless rope that does not stretch. Suppose further that a person is clipped to the rope by a carabiner, with all of their weight essentially supported at one point. Finally, suppose that the rope bridge is strung between anchor points that are separated by a horizontal distance of 12.0 m, and that the sag in the bridge when the person is at the midpoint is 1.20 meters.
Part A
If the person is at rest at the midpoint, what is the ratio of the tension in the rope to the person's weight?
Solution
System:
Interactions:
Model:
Approach:
Diagrammatic Representation
We begin with a picture of the situation:
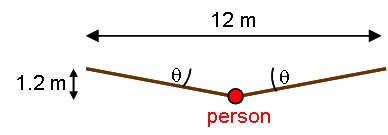
Note that at the midpoint, the rope will be symmetric. Thus, the angles on each side will be the same.
We next construct a free body diagram for the person:
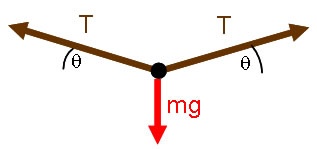
Note that tension appears twice. Again, the symmetry dictates that the tension on each side be the same.
Mathematical Representation
The person is at rest, so their acceleration is zero in both the x and y directions. The x-direction equation is clearly satisfied since we have assumed that the tension and rope angles on each side of the person are the same. Newton's 2nd Law for the y direction gives:
\begin
which is solved to give:
\begin
[ \frac
= \frac
] \end
The angle θ is determined by the length of the bridge and the amount of sag in the rope:
\begin
[ \theta = \tan^{-1}\left(\frac
\right) ] \end
Thus:
\begin
[ \sin\theta = \frac
{\sqrt{h^
}}]\end
and:
\begin
[ \frac
= \frac{\sqrt{h^
}}
= 2.55 ]\end
For a 180 lb person, this would correspond to a tension of about 460 lbs. Note that to achieve less sag, more tension must be provided.
Part B
Consider the same rope bridge. If the person is at rest exactly 1/6 of the way along the bridge (as measured horizontally) what is the tension in each side of the rope in terms of the person's weight? Assume that the length of the rope is constant.
Solution
System, Interactions and Model: As in Part A.
Approach:
Diagrammatic Representation
The new picture is:
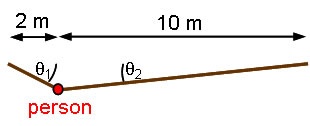
which gives the free-body diagram:
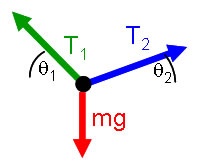
Note that now we do not have symmetry about the location of the person and so both the angles and the tensions can be different on the two sides.
Mathematical Repesentation
The equations of Newton's Law give:
\begin
[ T_
- T_
= 0 ]
[ T_
+ T_
- mg = 0]\end
These equations cannot be solved without further information. The extra information is the length of the rope. We know from Part A that the rope's length is:
\begin
[ 2\sqrt{h_
^
+ (L/2)^{2}} = \mbox
]\end
We can also write the length of the rope in terms of the sag of the rope at the 1/6 L point:
\begin
[ \mbox
= \sqrt{h_
^
+ (L/6)^{2}} + \sqrt{h_
^
+ (5L/6)^{2}} ]\end
which can be solved to give:
\begin
[ h_
= \mbox
]\end
Once hB is known, the equations of Newton's 2nd Law become:
\begin
[ T_
\frac
{\sqrt{h_
^
}} - T_
\frac
{\sqrt{h_
^
}} = 0][ T_
\frac{h_{B}}{\sqrt{h_
^
}} + T_
\frac{h_{B}}{\sqrt{h_
^
}} - mg = 0]\end
Eliminating T2 then gives:
\begin
[ \frac{T_{1}}
= \frac{5\sqrt{h_
^
}}{6h_{B}} = 2.17 ]\end
and solving for T2 gives:
\begin
[ \frac{T_{2}}
= \frac{\sqrt{h_
^
}}{6h_{B}}= 2.01 ]\end
These results are messy, and so it pays to put the answers back into the equations of Newton's 2nd Law to check them.
