You are viewing an old version of this page. View the current version.
Compare with Current
View Page History
« Previous
Version 49
Next »
Part A
Velodromes are indoor facilities for bicycle racing (picture by Keith Finlay, courtesy of Wikimedia Commons
). Olympic velodromes are usually ovals 250 m in circumference with turns of radius 25 m. The peak banking in the turns is about 42°. Assuming a racer goes through the turn in such a velodrome at the optimal speed so that no friction is required to complete the turn, how fast is the racer moving?
System: The rider will be treated as a point particle.
Interactions: The rider is subject to external influence from the earth (gravity) and from the track (normal force). We assume friction is not present, since we are told to determine the speed at which friction is unnecessary to complete the turn.
Model: Point Particle Dynamics.
Approach:
Diagrammatic Representation
Since we are assuming no friction is needed, we have the free body diagram and coordinate system shown above.
Mathematical Representation
The corresponding equations of Newton's Second Law are:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[\sum F_
Unknown macro: {x}
= N \sin\theta = \frac{mv^{2}}
Unknown macro: {r}
][\sum F_
Unknown macro: {y}
= N \cos\theta - mg = 0 ] \end
Where r is the radius of the turn, v is the speed of the racer and m is the racer's mass (including bike and gear).
From the y-component equation, we find:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ N = \frac
Unknown macro: {mg}
Unknown macro: {costheta}
]\end
Substituting into the x-component equation then gives:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ v = \sqrt
Unknown macro: {grtantheta}
= 15 \:
Unknown macro: {rm m/s}
= 33 \:
Unknown macro: {rm mph}
]\end
Part B
The Indianapolis Motor Speedway (site of the Indianapolis 500 race) has four turns that are each 0.25 miles long and banked at 9.2°. Supposing that each turn is 1/4 of a perfect circle, what is the minimum coefficient of friction necessary to keep an IndyCar traveling through the turn at 150 mph from skidding out of the turn? (Photo courtesy Wikimedia Commons, uploaded by user The359.)
System: The car plus contents will be treated as a point particle.
Interactions: The car will be subject to external influences from the earth (gravity) and from the track (normal force and friction).
Model: Point Particle Dynamics.
Approach:
Diagrammatic Representation
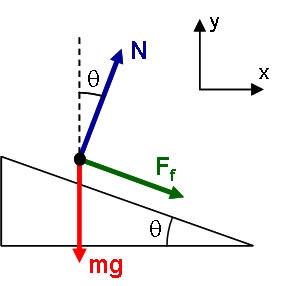
The free body diagram from Part A is modified to include friction, as shown above.
Mathematical Representation
The resulting form of Newton's Second Law is:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ \sum F_
Unknown macro: {x}
= F_
Unknown macro: {f}
\cos\theta + N \sin\theta = \frac{mv^{2}}
Unknown macro: {r}
][ \sum F_
Unknown macro: {y}
= N \cos\theta - F_
\sin\theta - mg = 0] \end
We have three unknowns (N, Ff, and m) but only two equations. To solve, we must develop another constraint. To do so, we must notice a key phrase in the problem statement. We are asked to find the minimum coefficient of friction. The minimum coefficient will be the value such that the static friction force is maximized, satisfying:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[F_
Unknown macro: {f}
= \mu_
Unknown macro: {s}
N ] \end
With this substitution, we have:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ \sum F_
Unknown macro: {x}
= \mu_
Unknown macro: {s}
N \cos\theta + N \sin\theta = \frac{mv^{2}}
Unknown macro: {r}
][ \sum F_
Unknown macro: {y}
= N \cos\theta - \mu_
N \sin\theta - mg = 0] \end
Proceeding as in Part A:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ N = \frac
Unknown macro: {mg}
{\cos\theta - \mu_
Unknown macro: {s}
\sin\theta} ]\end
which is then substituted into the y-component equation to give:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[\mu_
Unknown macro: {s}
\ge \frac{v^
Unknown macro: {2}
\cos\theta - gr \sin\theta}{v^
\sin\theta + gr \cos\theta}]\end
The substitutions here require some thought. The turns are quarter-circle segments with a length of a quarter mile each. Thus, they have the same radius of curvature as a full circle with circumference 1 mile. The corresponding radius is 256 meters. Then, converting the speed to m/s and using the formula derived above gives:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[\mu_
Unknown macro: {s}
\ge 1.3]\end
Unknown macro: {table}
Unknown macro: {tr}
Unknown macro: {td} [Examples from Dynamics]
Unknown macro: {tr}
Unknown macro: {td}
The root page Examples from Dynamics could not be found in space Modeling Applied to Problem Solving.
Unknown macro: {search-box}