The Integral Form of Newton's Second Law and Impulse
The Law of Change for the Momentum and External Force model can in principle be integrated:

The left hand side of this expression is simple, and after some rearrangement, the equation becomes:
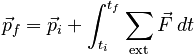
In principle, it might be useful to leave the integral over force explicit in this equation, but in practice it is not useful. If a known force which is an easily integrable function of time is applied, then it is usually just as simple and more intuitive to use the traditional F = ma approach (followed by regular kinematics).
The utility of this equation actually lies in the reverse approach: using what is known about momentum to learn about the force. To facilitate this, we define the impulse associated with a force as:
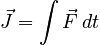
With this definition, the integral form of the Law of Change can be written:
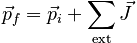
Off the Wall (Simple problem illustrating the definition of impulse and the utility of an initial-state final-state diagram.)

