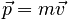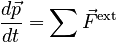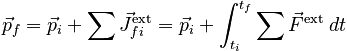Introduction to the Model
Description and Assumptions
This model is generally applicable (assuming knowledge of the external forces and system constituents). The model is especially useful when describing the momentum of systems where external forces are absent (system momentum will be constant) or estimating the force in a process that occurs in a very short time interval such as collisions (impulse will be easier to determine than force).
Learning Objectives
Students will be assumed to understand this model who can:
Relevant Definitions
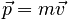
S.I.M. Structure of the Model
Compatible Systems
The system must be effectively composed of point particles, though rigid bodies may be treated as point particles with positions specified by the center of mass positions of the rigid body when this model is used.
Relevant Interactions
Only external forces need be considered, since internal forces do not change the system's momentum.
Laws of Change
Mathematical Representation
Diagrammatic Representations
Relevant Examples
Examples Involving Constant Momentum
-
Page:
-
Page:
Let it Rain
— Analyzing a continuous momentum flux (falling water).
-
Page:
-
Page:
Head-on Collision
— Compare the forces on the occupants of two cars in a 1-D totally inelastic collision.
-
Page:
A Walk on the Pond
— How far will two children slide after a perfectly inelastic collision?
-
Page:
Examples Involving Impulse
-
Page:
Watch Your Head
— Consider the impulse and average force delivered to the head of a player performing a "header" in soccer.
-
Page:
Head-on Collision
— Compare the forces on the occupants of two cars in a 1-D totally inelastic collision.
-
Page:
Examples Involving 1-D Collisions
-
Page:
Head-on Collision
— Compare the forces on the occupants of two cars in a 1-D totally inelastic collision.
-
Page:
Examples Involving 2-D Collisions
-
Page:
-
Page:
-
Page:
A Walk on the Pond
— How far will two children slide after a perfectly inelastic collision?
Examples Involving Elastic Collisions
Examples Involving Totally Inelastic Collisions
-
Page:
-
Page:
Head-on Collision
— Compare the forces on the occupants of two cars in a 1-D totally inelastic collision.
-
Page:
A Walk on the Pond
— How far will two children slide after a perfectly inelastic collision?
Examples Involving Continuous Momentum Flux
-
Page:
Let it Rain
— Analyzing a continuous momentum flux (falling water).
-
Page:
All Examples Using this Model
-
Page:
-
Page:
Let it Rain
— Analyzing a continuous momentum flux (falling water).
-
Page:
Head-on Collision
— Compare the forces on the occupants of two cars in a 1-D totally inelastic collision.
-
Page:
Watch Your Head
— Consider the impulse and average force delivered to the head of a player performing a "header" in soccer.
-
Page:
-
Page:
-
Page:
A Walk on the Pond
— How far will two children slide after a perfectly inelastic collision?
|



Photos courtesy:
|
html: Security restricted macro is not allowed. An edit restriction is required that matches the macro authorization list.
<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>