MIT 8.01 Lesson 4: 1-D Motion - General
Lesson Summary
We consider the motion of a point particle in one dimension, which can occur either because the particle is constrained to move along a track, or because we restrict attention of one Cartesian component of a particle's motion. In general, the force applied to this particle can vary arbitrarily with time. Hence the particle will have time-varying acceleration in proportion, a(t). The resulting motion may then be found using calculus: the velocity v(t) is the integral of the acceleration a(t) plus the velocity at the start of the interval of integration. Mathematically we'd say that the arbitrary constant of integration is constrained by the initial condition on the velocity. To get x(t) we integrate v(t) and add the initial position.
Learning Objectives
By the end of this Lesson, you should be able to:
- Read and understand the One-Dimensional Motion (General) model summary.
- Accomplish the Learning Objectives listed in that summary.
- Summarize the structure of the Hierarchy of models that fall under the One-Dimensional Motion (General) model, and state the specializations required for each sub-model to apply.
Introduction
The quantities v(t) and a(t) are important in physics because these mathematically defined quantities appear in experimentally discovered physical laws. The acceleration is related to the force applied via F=ma, and the velocity determines things like the Doppler Shift and the pressure measured in a Pitot tube - those little bent tubes that stick out of fuselage of an airplane and are bent to face into the airflow so that a pressure-measuring instrument can determine the plane's airspeed.
In our hierarchy of models there are two mutually exclusive special cases: Simple Harmonic Motion caused by a restoring force that varies linearly with the particle's displacement from some center of force, and Motion with Constant Acceleration, caused by a constant force. Motion with Constant Velocity is a special case of Motion with Constant Acceleration specified by the constraint a(t) = 0.
Definitions of Position and Velocity
If we start knowing the position vs. time x ( t ), then the velocity, v ( t ), is the derivative of its position, and the derivative in turn of this velocity is the particle's acceleration, a ( t ). The force is the particle's mass times a ( t ).
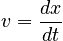
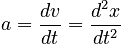
In fact, as you can see, the velocity and acceleration are defined as derivatives of the position, a fact acknowledged by the phrase "the calculus of motion". Newton had to invent calculus of one variable to deal with motion!
Integration of the Definitions in Special Cases
General Time Integrals
The defnitions of the acceleration and velocity can be integrated, provided something is known about the functional form of the acceleration. The general procedure is to first find the velocity as a function of time by integrating the acceleration:
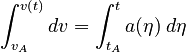
We are using η as the dummy variable of integration on the right because we are using t as the (arbitrary) endpoint of the integration, and so t is not available as the integration variable. You can just as easily use any other dummy variable.
and then use that velocity in the integral:
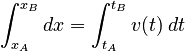
Two basic forms of the acceleration are widely useful and so we illustrate the procedure for these as special cases.
Case 1: Constant Acceleration
If the acceleration is constant then the velocity has the form:
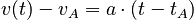
which is substituted into the next integral to find:
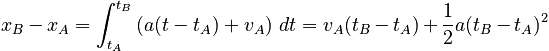
This equation is the basic Law of Change for the One-Dimensional Motion with Constant Acceleration model.
Does this agree with the Law of Change of the One-Dimensional Motion with Constant Velocity model for the special case a = 0?
Case 2: Acceleration Varying Linearly with Position
The procedure illustrated above will work for any acceleration which given as an explicit and integrable function of time (though of course some integrable functions require more work to integrate than others). The procedure must be modified, however, if the acceleration is given as an implicit function of time. The simplest such specification that is commonly encountered in mechanics is:
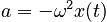
where ω is a (real number) constant. Because the acceleration depends implicitly on time through the unknown time dependence of the position, we must solve for the position by construcing a second-order differential equation:
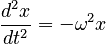
Solving a differential equation often requires specialized techniques, but in some simple cases (like this one) a good calculus student can guess the answer based upon the properties of common functions. In this case, the fact that the trig functions sine and cosine are proportional to the negative of their own second derivative is a big clue that the answer can be given in terms of these functions. We will explore the solutions to this differential equation in more detail when we learn the Simple Harmonic Motion model.
The character of the equation changes dramatically if the negative on the right hand side is removed, and sine or cosine is no longer a solution. The answer is still readily guessed by a student familiar with the basic functions of calculus, however. Can you think of a common function which would solve the case when the right hand side is positive?
Specializations and the Hierarchy of Models
The fact that we will study the two specializations discussed above in detail means that it makes sense to consider them separate models even though they are clearly special cases of the One-Dimensional Motion (General) model. Thus, if you examine the hierarchy of Models, you will see these two special cases listed below the General motion case as One-Dimensional Motion with Constant Acceleration and Simple Harmonic Motion. Of course, we could generate an infinite number of special cases, such as accelerations that are polynomial functions of time, accelerations that are proportional to velocity, and so on. In the hierarchy, we present only the specializations that are commonly taught and used in introductory mechanics. If you take a more advanced course in mechanics, you may want to expand the hierarchy to incorporate new specializations.
One-Dimensional Motion (General) - System: One point particle constrained to move in one dimension. — Interactions: Any that respect the one-dimensional motion.
- 1-D Motion (Constant Acceleration) — System: One point particle moving in one dimension either because it's constrained to move that way or because only one Cartesian component is considered. — Interactions: Constant force (in magnitude or in its component along the axis).
- 1-D Motion (Constant Velocity) — System: One point particle. — Interactions: No acceleration (zero net force).
- Simple Harmonic Motion — System: One point particle constrained to move in one dimension. — Interactions: The particle must experience a force (or torque) that attempts to restore it to equilibrium and is directly proportional to its displacement from that equilibrium.
