Mass on a Vertical Spring

Part A

Consider first the static case with the mass hanging from the spring and not moving.

Solution

System:

Simple Harmonic Motion.

Interactions:

The forces due to the compression or extension of the two springs acting as the restoring force and the force of gravity (near-earth).

Model:

Simple Harmonic Motion.

Approach:

Diagrammatic Representation

The mass m is suspended from a perfect spring with force constant k . Attaching the mass stretches the spring a distance a from its equilibrium length. Draw the force diagram and determine what a must be.

Mathematical Representation

We first consider the case of a stationary mass on a vertical spring. Adding the mass causes the spring to extend a distance a beyond its "neutral", unstretched length. After the mass has come to rest, what are the forces?

From the above diagram, we have the force of gravity pulling downwards with F_g = mg and the spring force pulling upwards with force F_s = ka . Since the mass is stationary we must have

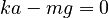
we can solve for the displsacement at equilibrium:

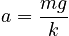
Part B

Analyze the forces on the mass as it oscillates up and down and give its equation of motion.

Solution

System:

Simple Harmonic Motion.

Interactions:

The forces due to the compression or extension of the spring acting as the restoring force and the force of gravity (near-earth).

Model:

Simple Harmonic Motion.

Approach:

Diagrammatic Representation

The mass m is now displaced from its equilibrium position (extended by a distance a) by an additional distance x .

Mathematical Representation

Displacing the mass a distance x downwards results in restoring force from the spring. We calculated the total force on the mass, due to the original extension and this additional extension, as well as by gravity. we obtain the upward force

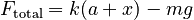
But we know from the previous section that ka = mg, so the first and last terms will cancel, leaving

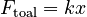
just as in the case of a horizontal spring and mass on a frictionless surface (see, for example, the worked example Mass Between Two Springs)The solution for the equation of motion is, as in the case of Simple Harmonic Motion

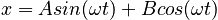
where

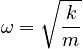
and A and B are determined by the initial conditions, the initial position x_i and the initial velocity v_i

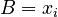
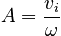
These are exactly the same angular velocity and coefficients A and B as in the case of the horizontal mass on a spring (in the absence of gravity).

Part C

What if we look at the problem from the point of view of energy. How can the energy be conserved in the same way as a horizontal mass on a spring if we have to consider Gravitational Potential Energy as well?

Solution

System:

Simple Harmonic Motion.

Interactions:

The forces due to the compression or extension of the two springs acting as the restoring force and the force of gravity (near-earth).

Model:

Simple Harmonic Motion.

Approach:

Diagrammatic Representation

Mathematical Representation

Consider the total energy relative to the spring's neutral position, where it is neither extended nor comprseed. Even for the static situation of Part A, then, the system has stored energy, since you have extended the spring. On the other hand, the mass has fallen, and so you have lost some potential energy due to gravity. The total energy change is ΔE₁:

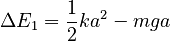
If you now displace the mass downward by a distance x_i and hold onto it you change the overall energy because you have done work on the system (you've exerted force against the spring over a distance x_i, and you've also lost gravitational potential energy in moving downwards). The new energy relative to the neutral position is ΔE₂

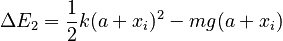
From Part A we know that a = mg/k , so, substituting:

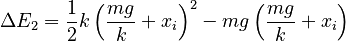
Expanding this, then consolidating terms yields

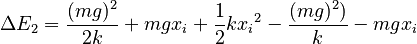
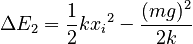
Now consider the energy when the mass has rebounded and is at the original location a. It is now moving at velocity v and the total energy, potential and kinetic, is

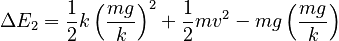
or

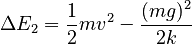
Comparing these two equations, we have that, aside from a constant term of * - (mg)²/2k* , the Kinetic Energy at the "equilibrium" position is simply * (1/2) m v² * and the Potential Energy at full extension (aside from that same constant term) is (1/2) k {x_i}² , so the emergies are, except for this constant offset term, the same as those for a horizontal spring and mass. Choosing the position at which we calculate zero energy properly would completely eliminate this superfluous term. The vertical spring and mass behaves exactly like a horizontal one in both force and energy relationships, despite the presence of gravity (interaction).