Calculate the moment of inertia of a solid sphere of radius R and uniform density ρ rotated about an axis passing through its center.
Solution
System, Interactions and Model: Not applicable. We solve this problem using the definition of the moment of inertia.
Approach: We will have to perform an integral over the volume of the sphere to calculate the moment of inertia. The integral is best performed in cylindrical coordinates with the z-axis chosen to lie along the axis of rotation, since it takes the form:
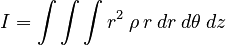
In spherical coordinates, the integrand is complicated by the fact that the radial coordinate measures deviation from the center point instead of the axis of rotation.
The best way to configure this integral is to integrate over angle first, then radius, and finally the z-coordinate. The sphere is continuous so the limits on theta are always zero to 2
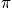
, and the sphere is axially symmetric so the integrand has no dependence on θ. Thus, we can simply perform this integral to obtain:
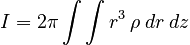
It is simplest to next perform the integral over r. Here we have some trouble, however, since the limits on r will be a function of z. Basically, we are cutting the sphere up into a stack of circles perpendicular to the z-axis. If we move through the stack from bottom to top, the circles first grow larger (as we near the center) and then reduce in size again until their radius disappears at the "north pole" (the top of the sphere). Based upon the well-known definition of a spherical surface in rectangular coordinates:
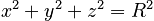
and using the relationship between cylindrical coordinates and rectangular coordinates:
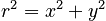
we can see that the radius of the circle perpendicular to the z-axis at a given z-value will be:
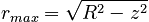
Thus, we can set up the limits of our integral as:
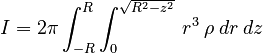
Performing the r integral gives:
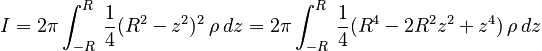
and finishing with the z integral:
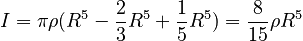
The answer can be put in terms of the mass of the sphere by noting that for a uniform sphere:
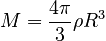
so:
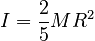
<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>