Newton's Third Law

Every force exerted on one body by a second body is paired with another force of equal magnitude and opposite direction exerted on the second body by the first.

Motivation for Concept

It is impossible for one object to alter the motion of another without in turn having its own motion altered. The object that "instigated" the collision is at no fundamental advantage. (Consider how much easier it would be to assign fault in a traffic accident without the Third Law.) You can feel the consequences of Newton's Third Law by kicking a heavy object. You can see the consequences by sitting next to another person on wheeled chairs and experimenting with what happens when one person pushes the other.

Statement of the Law

Newton's Statement

"To any action there is always an opposite and equal reaction; in other words, the actions of two bodies upon each other are always equal and always opposite in direction." (The Principia by I. Newton, translated by I.B. Cohen and A. Whitman.)

Modern Statement

Through careful consideration, every force can be assigned two "participant" bodies. One body is the originator of the force, the other is acted upon by the force. Thus, any force can technically be assigned two indices. A force on object A that originates from object B can be denoted F_AB. Newton's Third Law says that for any F_AB, there will of necessity be an F_BA related by:

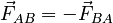
Use in Problem Solving

Free Body Diagrams

The most important consequence of Newton's 3rd Law is in setting up the equations of Newton's 2nd Law. This is usually done with the aid of a free body diagram. If a problem requires you to construct free body diagrams for more than one object, it is vital to remember to apply Newton's 3rd Law to any forces acting on one body of interest that arise from another body of interest.

Cancellation of Internal Forces

In the simultaneous equations resulting from Newton's 2nd Law applied to more than one object, the forces that act on one body of interest that arise from another body of interest can always be eliminated from the system trivially as a consequence of Newton's 3rd Law. Thus, if the bodies are combined into a single system, these internal forces drop out of the equations of Newton's 2nd Law for that system.

Conservation of Momentum

The constancy of the momentum of a system composed of many bodies that is isolated from external influences is a direct consequence of Newton's 3rd Law applied to Newton's 2nd Law. Because internal forces drop out of Newton's 2nd Law for the system, the system's momentum will be constant.

The Horse and Cart "Paradox"

Statement of the "Paradox"

Consider a trailer attached to a car. If the car pulls on the trailer with a force F in an attempt to drive away, Newton's 3rd Law guarantees that the trailer will pull back on the car with the same force F. How, then, can the car pull the trailer?

Resolution of the "Paradox"

The paradox is easily resolved if the forces are specified completely. The car exerts a force F_TC on the trailer and the trailer exerts a force F_CT on the car. The free body diagrams for the car and trailer including only these forces would look like:

In one sense, we have already resolved the paradox. The forces do not cancel, since they act on separate bodies! In another sense, however, we still have to worry about the diagrams we have made. It seems the car will be pulled backward while the trailer moves forward. Indeed, in the absence of other forces, this would be the result (consider a tug-of-war in space). We must not forget, however, that the engine is turning the car's wheels which rub against the ground. Thus, the car's free body diagram must have (at least) the modification:

where F_CG is the force acting on the car from the ground's friction with the car's tires. We now see that as long as the friction between the car's tires and the ground (a result of the action of the car's engine trying to turn the wheels) is larger than F_CT, both the car and the trailer will move forward.