A 220 lb running back is running along the sideline of the football field toward the goal line. The running back is 1.0 m from the sideline running at 8.0 m/s toward the goal. A 180 lb defender runs across the field toward the running back 2.0 m from the goal line. Just before the collision, both players leap into the air. The running back's horizontal speed remains 8.0 m/s. When the players collide, the defender clings to the running back resulting in a totally inelastic collision. What is the minimum possible horizontal velocity for the defender in order to ensure the players cross out of bounds before crossing the goal line?
Solution
System:
Interactions:
Model:
Approach:
Diagrammatic Representation
We are interested only in the horizontal components of the velocity. If we treat the players as point masses, then the defender's goal is for the horizontal velocity after the collision to be directed at a minimum of 27 degrees (the inverse tangent of 1/2) from the running back's original direction of motion, as shown in the figure.
It is important to understand that the 1m and 2m legs of the triangle drawn in black are not the components of the final velocity. They are distances, not velocities. The vector triangle formed by the final velocity (shown in purple) and its x- and y- components must be similar (in the mathematical sense) to the distance triangle for the critical case in which both players pass over the point of intersection between the Goal Line and the Out of Bounds Line. Thus, in this case, the angle in the distance triangle (27° for the given distances) must be the same as the angle of the velocity vector. Of course, the Defending Player will want to be travelling faster than this, to be certain that the opposing player is driven out of bounds before he crosses the goal line!
Mathematical Representation
Since we are assuming external forces are negligible during the collision, we will have constant horizontal momentum:
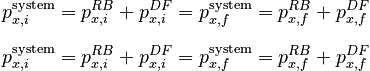
where RB denotes the running back and DF the defender. For the case at hand, these equations can be simplified to read:
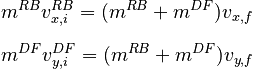
We can immediately solve the x direction equation:
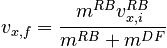
but the y equation contains two unknowns. We can resolve this problem by using the constraints (discussed above) that in order to end up out of bounds:
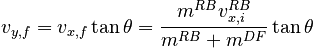
With this information, we can solve to find:
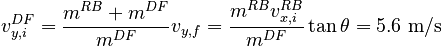
so that the horizontal component of the defender's velocity must be at least 5.6 m/s.
Note that our formula indicates that a larger angle will require a larger speed for the defender.

