h3. Part B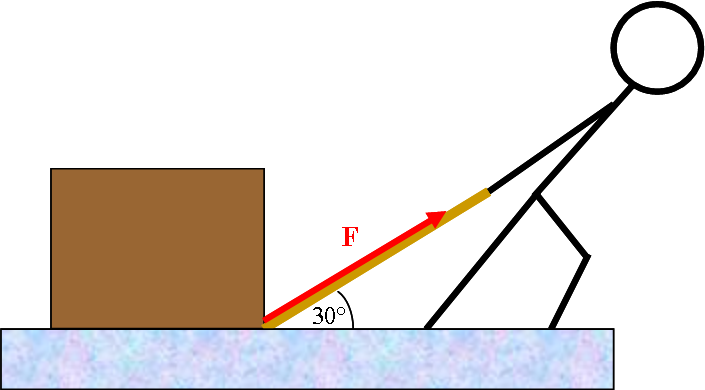 Image Added Image Added
A person pulls a box of mass 15 kg along a smooth floor by applying a force F at an angle of 30° above the horizontal.. The box accelerates horizontally at a rate of 2.0 m/s2. What is the magnitude of F? Solution System: Interactions: | Cloak |
|---|
| External influences from the person (applied force) the earth (gravity) and the floor (normal force). |
Model: Approach: Diagrammatic Representation Before writing Newton's 2nd Law for the x direction, we choose coordinates and break the applied force F into x- and y-components: 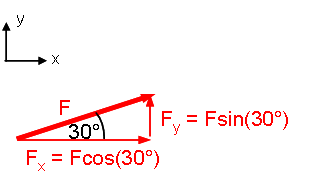 Image Added Image Added
Mathematical Representation The free body diagram implies: | Latex |
|---|
B
!pushblock2_2.png|width=400!
A person pulls a box of mass 15 kg along a smooth floor by applying a force _F_ at an angle of 30° above the horizontal.. The box accelerates horizontally at a rate of 2.0 m/s{color:black}^2^{color}. What is the magnitude of _F_?
h4. Solution
{toggle-cloak:id=sysb} *System:* {cloak:id=sysb} Box as [point particle].{cloak}
{toggle-cloak:id=intb} *Interactions:* {cloak:id=intb} External influences from the person (applied force) the earth (gravity) and the floor (normal force).{cloak}
{toggle-cloak:id=modb} *Model:* {cloak:id=modb}[Point Particle Dynamics].{cloak}
{toggle-cloak:id=appb} *Approach:*
{cloak:id=appb}
{toggle-cloak:id=diagb} {color:red} *Diagrammatic Representation* {color}
{cloak:id=diagb}
Before writing [Newton's 2nd Law|Newton's Second Law] for the _x_ direction, we choose coordinates and break the applied force _F_ into x- and y-components:
!pushingboxmore2.png!
{cloak:diagb}
{toggle-cloak:id=mathb} {color:red} *Mathematical Representation* {color}
{cloak:id=mathb}
The free body diagram implies:
{latex}\begin{large}\[ \sum F_{x} = F\cos\theta = ma_{x}\] \end{large}{latex}
|
Solving for _F _:
{| Latex |
|---|
}\begin{large}\[ F = \frac{ma_{x}}{\cos\theta} = \mbox{34.6 N}\]\end{large}{latex}
{cloak:mathb}
{cloak:appb}
| |