Unknown macro: {td}

A bucket for collecting water from a well is suspended by a rope which is wound around a pulley. The empty bucket has a mass of 2.0 kg, and the pulley is essentially a uniform cylinder of mass 3.0 kg on a frictionless axle. Suppose a person drops the bucket (from rest) into the well.
Part A
What is the bucket's acceleration as it falls?
Solution
We will consider two different methods to obtain the solution.
Systems:
The pulley and the bucket are treated as separate objects. The bucket can be treated as a point particle, but the pulley must be treated as a rigid body.
Interactions:
The pulley and the bucket are each subject to external influences from the rope and from [gravitation]. The pulley is also subject to a force from the axle.
Model:
Single-Axis Rotation of a Rigid Body and Point Particle Dynamics
Approach:
Diagrammatic Representation
We begin with free body diagrams for the two objects.
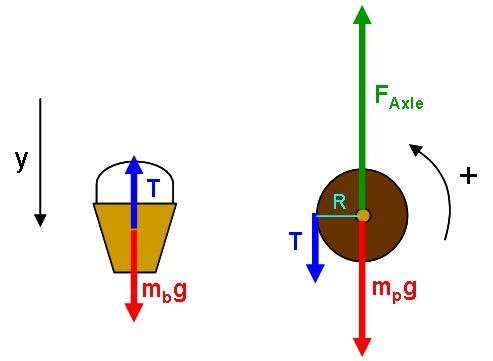
Mathematical Representation
For the bucket, we write Newton's 2nd Law:
Unknown macro: {latex} \begin
Unknown macro: {large} [ m_
Unknown macro: {b} g - T = m_
a_
Unknown macro: {b}
] \end
For the pulley, there will be no translation, only rotation about the center of mass. We sum the torques about the fixed axis defined by the axle:
Unknown macro: {latex} \begin
Unknown macro: {large} [ TR = I_
Unknown macro: {p} \alpha_
] \end
We now make the assumption that the rope does not stretch or slip as it unwinds. These assumptions allow us to relate the rotation rate of the pulley to the motion of the bucket:
Unknown macro: {latex} \begin
Unknown macro: {large} [ \alpha_
Unknown macro: {p}
R = a_
Unknown macro: {b}
]\end
With this assumption, we can solve the system of equations to obtain:
Unknown macro: {latex} \begin
Unknown macro: {large} [ a_
Unknown macro: {b} = \frac
Unknown macro: {g}
{1+\frac{\displaystyle I_{p}}{\displaystyle m_
R^
Unknown macro: {2}
}} ] \end
or, using the formula for the moment of inertia of a cylinder:
Unknown macro: {latex} \begin
Unknown macro: {large} [ a_
Unknown macro: {b} = \frac
Unknown macro: {g}
{1+\frac{\displaystyle m_{p}}{\displaystyle 2m_
}} = \mbox
Unknown macro: {5.6 m/s}
^
Unknown macro: {2}
]\end
System:
An alternate approach is to combine the bucket and the pulley into a single system.
Interactions:
The system is subject to external forces from the earth acting on the bucket and the pulley (gravity) and from the axle acting on the pulley (contact force). If we choose the axis of rotation to coincide with the axle of the pulley, then the axle's force and gravity acting on the pulley each produce no torque. We need only consider the effects of gravity acting on the bucket.
Model:
Angular Momentum and External Torque about a Single Axis
Approach:
The angular momentum of the system can be expressed by summing the angular momentum of the parts. The pulley's contribution is Ip ωp. The bucket can effectively be treated as a point particle, so it will contribute:
Unknown macro: {latex} \begin
Unknown macro: {large} [ L_
Unknown macro: {rm axis}
= m\vec
Unknown macro: {r}
_
Unknown macro: {rm cm,axis}
\times\vec
Unknown macro: {v}
_
Unknown macro: {rm cm}
] \end
The total angular momentum is:
Unknown macro: {latex} \begin
Unknown macro: {large} [ L_
Unknown macro: {rm system}
= I_
Unknown macro: {p} \omega_
+ m_
Unknown macro: {b} v_
R ]\end
We now assume that the rope does not stretch or slip, allowing us to relate the rotational speed of the pulley to the speed of the bucket as it falls:
Unknown macro: {latex} \begin
Unknown macro: {large} [ \omega_
Unknown macro: {p}
R = v_
Unknown macro: {b}
]\end
We then set the sum of external torques equal to the change in angular momentum of the system:
Unknown macro: {latex} \begin
Unknown macro: {large} [ m_
Unknown macro: {b} gR = \frac
Unknown macro: {d}
Unknown macro: {dt}
\left(I_
Unknown macro: {p}
\frac{v_{b}}
Unknown macro: {R}
+ m_
v_
Unknown macro: {b}
R\right)] \end
Now, using the fact that
Unknown macro: {latex} \begin
Unknown macro: {large} [ a_
Unknown macro: {b}
= \frac{dv_{b}}
Unknown macro: {dt}
] \end
lets us solve to find:
Unknown macro: {latex} \begin
Unknown macro: {large} [ a_
Unknown macro: {b} = \frac
Unknown macro: {g}
{1 + \frac{\displaystyle I_{p}}{\displaystyle m_
R^
Unknown macro: {2}
}} ] \end
deck: com.atlassian.confluence.macro.MacroExecutionException: java.lang.NullPointerException
Part B
What is the bucket's speed after falling 5.0 m down the well?
Solution
Again, we will use two methods.
Method 1
System:
Bucket as point particle.
Interactins:
External influences from the earth (gravity) and the rope (tension).
Model:
One-Dimensional Motion with Constant Acceleration.
Approach:
To use this method, you must first find the acceleration of the bucket using one of the methods of Part A. Once that acceleration is in hand, the problem is reduced to kinematics. The most direct solution is obtained by using:
Unknown macro: {latex} \begin
Unknown macro: {large} [v_
Unknown macro: {y} ^
Unknown macro: {2} = v_{y,{\rm i}}^
+ 2 a_
(y-y_
Unknown macro: {rm i}
) ] \end
If we assume y = 0 m at the height of release, then:
Unknown macro: {latex} \begin
Unknown macro: {large} [ v_
Unknown macro: {y} = \pm \sqrt{2 a_
y} ] \end
The speed of the bucket, then, must be:
Unknown macro: {latex} \begin
Unknown macro: {large} [ v_
Unknown macro: {b}
= \sqrt{2 (\mbox
Unknown macro: {5.6 m/s}
^
Unknown macro: {2}
) (\mbox
Unknown macro: {5.0 m}
)} = \mbox
Unknown macro: {7.5 m/s}
] \end
Method 2
System:
Treat the bucket, pulley and the earth as a single system.
Interactions:
Internal interactions of gravity (conservative) and tension from the rope (non-conservative) plus an external influence from the normal force on the pulley (non-conservative).
Model:
[Mechanical Energy and Non-Conservative Work].
Approach:
There will be no net non-conservative work on this system, even though there are non-conservative forces present. The normal force is a non-conservative external force, but does no work since the pulley experiences no displacement and the normal force has no moment arm and so exerts no torque. The tension forces on the pulley and the block are non-conservative internal forces. The tension forces do perform work on the system, but the work done by the downward tension on the pulley and the upward tension on the block are equal in size and opposite in sign. Therefore, their contributions cancel each other to give zero net non-conservative work.
We can now use the conservation of energy, which consists of three parts:
Unknown macro: {latex} \begin
Unknown macro: {large} [ K_
Unknown macro: {rm trans,i}
+ K_
Unknown macro: {rm rot,i}
+ U_
Unknown macro: {rm g,i}
= K_
Unknown macro: {rm trans,f}
+ K_
Unknown macro: {rm rot,f}
+ U_
Unknown macro: {rm g,f}
] \end
If we set h= 0 to be at the initial position of the bucket, then we can write:
Unknown macro: {latex} \begin
Unknown macro: {large} [ m_
Unknown macro: {p} g(-y_
Unknown macro: {a}
) = \frac
Unknown macro: {1} Unknown macro: {2} m_
Unknown macro: {b} v_
^
+ \frac
Unknown macro: {2}
I_
\omega_
Unknown macro: {p} ^
Unknown macro: {2}
+ m_
Unknown macro: {b} g(-y_
) + m_
g(-y_
Unknown macro: {a}
) ] \end
where ya denotes the (constant) vertical position of the center of mass of the pulley. Substituting using the relationship:
Unknown macro: {latex} \begin
Unknown macro: {large} [ \omega_
Unknown macro: {p}
R = v_
Unknown macro: {b}
]\end
gives
Unknown macro: {latex} \begin
Unknown macro: {large} [ m_
Unknown macro: {b} g y_
= \frac
Unknown macro: {1} Unknown macro: {2} m_
Unknown macro: {b} v_
^
+ \frac
Unknown macro: {2} I_
Unknown macro: {p}
\left(\frac{v_{b}}
Unknown macro: {R}
\right)^
]\end
We can now solve for vb (selecting the positive root since we are finding a speed):
Unknown macro: {latex} \begin
Unknown macro: {large} [ v_
Unknown macro: {b} = \sqrt{\frac{2 g y_{b}}{1 + \frac{\displaystyle I_{p}}{\displaystyle m_
R^{2}}}} = \mbox
Unknown macro: {7.5 m/s}
] \end
deck: com.atlassian.confluence.macro.MacroExecutionException: java.lang.NullPointerException
deck: com.atlassian.confluence.macro.MacroExecutionException: java.lang.NullPointerException

