Introduction
In all thermal systems, inequities in radiative heating lead to convective or conductive processes in fluid or solid bodies respectively in an effort to evenly distribute heat energy throughout the object. The earth is no exception, and the impetus of myriads of meteorological and oceanological phenomena that exhibit turbulence in this system can often be traced back to attempts of nature to evenly distribute the energy obtained through incident solar radiation.
Conceptual Visualization: The Earth
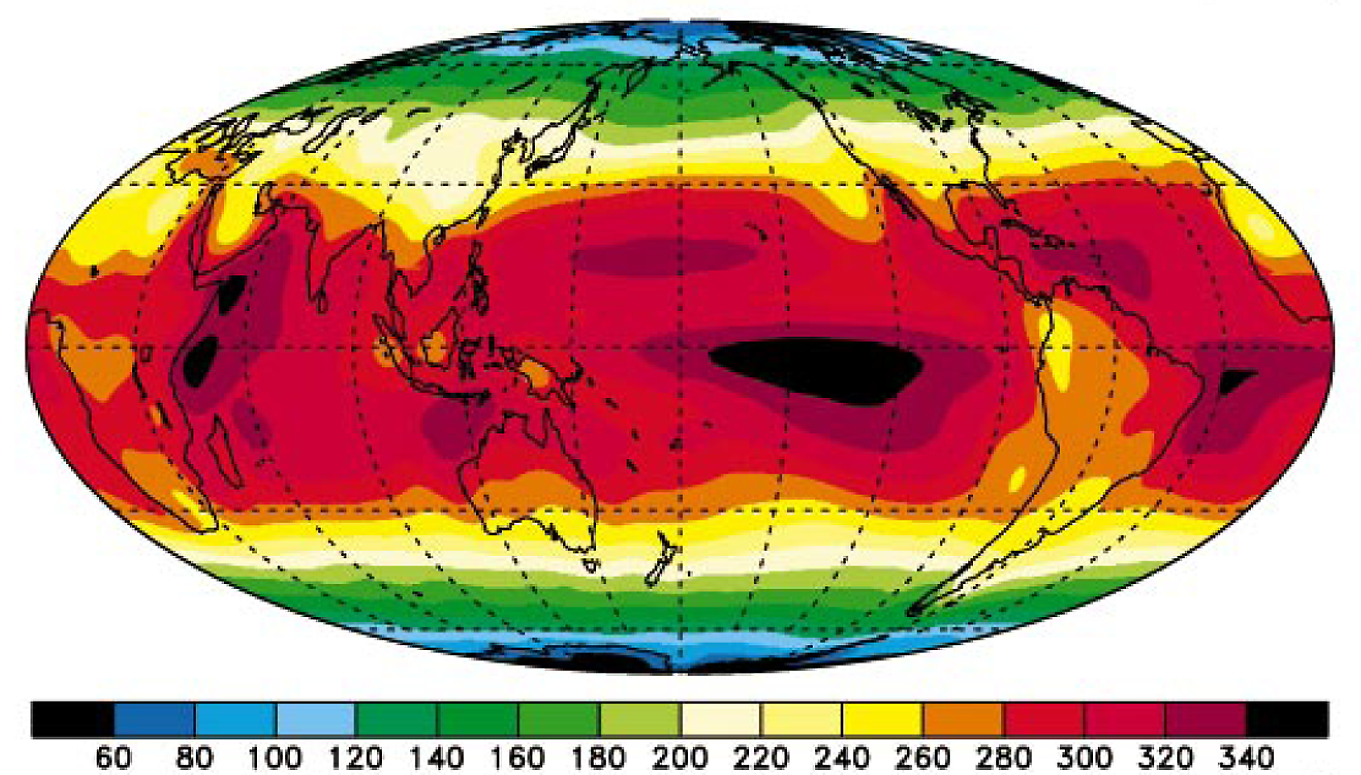
Figure 1.1: Figure from Trenberth and Stepaniak (2003). Copyright 2003 American Meteorological Society (AMS); http://www.climate.be/textbook/chapter2_node6.html
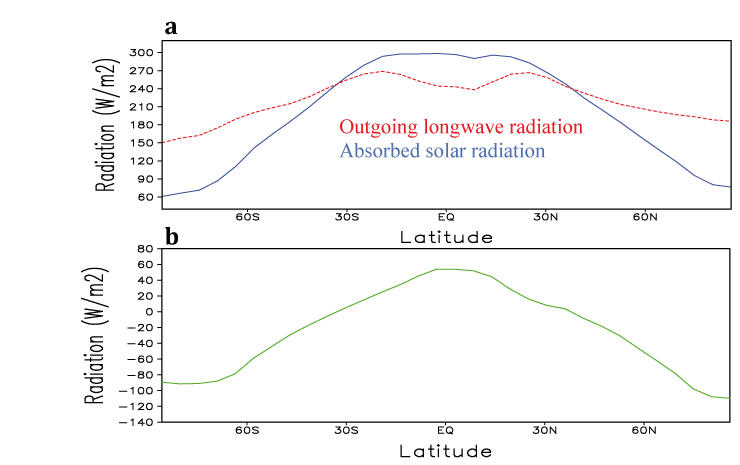
Figure 1.2: Cumulative sum of incoming and outgoing radiation with respect to latitude. http://www.climate.be/textbook/chapter2_node6.html
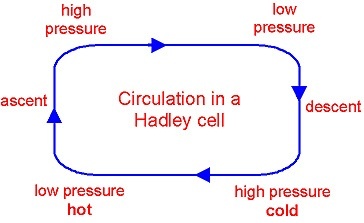
Given this, it would be sensible to conclude that thermal energy would be convected away from the equator and towards the poles. As such, the concept of the "Hadley Cell" is introduced, as is visible in Figure 1.3. At its root a horizontal circulation that serves as a "conveyer belt" for thermal energy, significant differences in the cell's behavior can be expected depending on whether or not the fluid is laminar or turbulent.
Figure 1.3: At its simplest, a thematic of a Hadley cell. http://www.elgheko.us/meteo.htm
Theory: Laminar or Turbulent Fluid, and Resultant Atmospheric Effects
Given that air should rise near the equator and sink in the vicinity of the polar regions, in a non-rotating system one would expect the motion of fluid to be purely meridional, towards the poles in the upper levels, and away from the poles and directed equatorially at the surface. However, the earth is a rotating system, with the atmosphere roughly in solid-body rotation. Therefore, we must take this into consideration, and do so using the Coriolis parameter. Because the Coriolis deflection is weakest at the equator and considering that fluid at the equator orbits the globe where its radius is the greatest, its angular momentum is greater than at any other point on earth since the earth is a solid body. Therefore, by the conservation of angular momentum, we would expect that, to conserve momentum, a parcel of air from the equator attempting to move towards the pole would be deflected eastward in direction since its zonal velocity must increase. Therefore, at the upper levels, a westerly jet should form, strongest as one heads away from the equator. For the sinking air later in its poleward journey, the opposite should be true; as it returns towards the equator, its weakening horizontal velocity due to the increase in radius should lead to surface easterly forming, strongest at the equator. This gives rise to the Intertropical Convergence Zone, where both Hadley cells converge. The rising motion here, coupled with the easterly winds (and the subtropical easterly jet, which, due to surface friction, is considerably weaker than other jets) leads to the development of tropical waves, and is an integral portion of cyclone forecasting.
When the Coriolis parameter is low, the fluid will be mainly laminar, and be governed by the physics of the Hadley cell. However, the entire globe cannot exist as a Hadley cell; proof of this can be sought within the Law of Conservation of Angular Momentum. Given that the radius of a parcel's orbit would be zero at the poles, utilizing solely this law would yield infinite winds aloft at those locations. Given that this is quite impossible, we are forced to rely on eddy heat transport, which "takes care of angular momentum" in other ways.
//This is where somebody better than me does their equation magic...