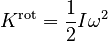The fundamental manifestation of mechanical energy, kinetic energy is the energy associated with an object's translational and/or rotational motion. Kinetic energy provides the definition of work (and hence all other forms of mechanical energy) through the Work-Kinetic Energy Theorem.
Mathematical Definition
Translational Kinetic Energy of a Point Particle
The kinetic energy of a point particle is given by:
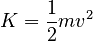
Translational Kinetic Energy of a System
Since energy is a scalar, the kinetic energy of a system of point particles is the sum of the kinetic energies of the constituents:
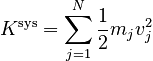
where N is the number of system constituents.
Kinetic Energy of a Rigid Body
Consider a rigid body that can rotate and translate. We begin by treating the rigid body as a collection of point masses that are translating with the center of mass of the body and also rotating about it with angular velocity ω. We therefore write the velocity of each point as a sum of rotational and translational parts:
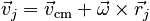
where rj is the position of the jth particle measured from the body's axis of rotation passing through the center of mass.
With this split, the kinetic energy of the body becomes:
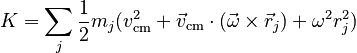
The center term will equal zero, because ω and vcm are constants, so:
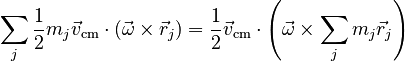
and the sum over mjrj is constrained to equal zero because we have assumed the center of mass is at the position r = 0 in our coordinates. With this realization, and using the definition of the moment of inertia, we have:
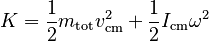
This result shows that the kinetic energy of a rigid body can be broken into two parts, generally known as the translational part and the rotational part.
Rotational Kinetic Energy
The above formula suggests a definition for the kinetic energy of a rotating body: