An interaction which produces a change in the energy of a system.
Page Contents |
|---|
Motivation for Concept
It requires effort to alter the energy of an object, as can clearly be seen by attempting to impart kinetic energy by pushing a car which has stalled or to impart [gravitational potential energy] by lifting a heavy barbell. We would like to quantify what we mean by "effort". It is clear that force alone is not enough to impart energy. Suppose that the car or the barbell is just too heavy to move. Then, for all the pushing or pulling that is done (a considerable force), no energy is imparted. For the energy of a system to change, the system must alter its position or its configuration. In effect, the force must impart or reduce motion of the object to which it is applied.
Mathematical Definition
Work-Kinetic Energy Theorem as Postulate
Suppose that we postulate the Work-Kinetic Energy Theorem for a point particle as the defining relationship of work. Doing so will allow us to find a mathematical definition of work in terms of force.
The relationship between the kinetic energy of a point particle and the work done on the point particle. This theorem is one way to arrive at a mathematical definition of work.Statement of the Theorem
If all the influences on a point particle are represented as works, the net work done by the forces produces a change in the kinetic energy of the particle according to:
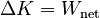
Derivation of the Theorem
From Newton's 2nd Law for a point particle, we know
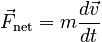
Now suppose that the particle undergoes an infinitesimal displacement dr. Since we want to bring the left side of the equation into line with the form of the expression for work, we take the dot product of each side with the displacement:

Before we can integrate, we make a substitution. Since v is the velocity of the particle, we can re-express the infinitesimal displacement as:
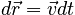
Making this substitution on the right hand side of the equation, we have:
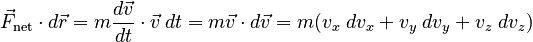
We can now integrate over the path:
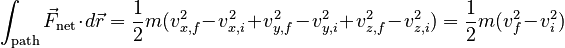
which is equivalent to the Work-Kinetic Energy Theorem.
Definition of Work
By comparing the derivation of the theorem to its statement, we see that in order for the theorem to be satisfied, we must make the definition:
\begin
[ W_
= \int_
\vec
_
\cdot d\vec
]\end
which leads us to define the work done by an individual force as:
\begin
[ W = \int_
\vec
\cdot d\vec
]\end
Importance of Path
Conservative Forces
The form of our definition of work involves a path integral. For some forces, however, the value of the path integral is determined solely by its endpoints. These forces are, by definition, [conservative forces]. This path-independence is the property which allows us to define a potential energy to associate with the force. Thus, the work done by conservative forces will usually be ignored, since their interaction is instead expressed as a contribution to the mechanical energy of the system. The two commonly considered conservative forces in introductory mechanics are:
- [gravity]
- spring forces
Non-Conservative Forces
Common forces in introductory physics whose effects are usually path dependent are:
For these forces, the path of the system must be understood in order to compute the work.
Example of Friction
To see the dependence of non-conservative work on path, consider a box moving along a rough, level surface. Suppose the box is subject only to horizontal applied forces, gravity, normal force and kinetic friction as it moves.