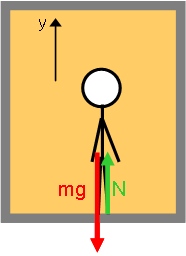
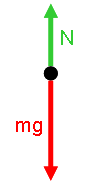One way that we perceive weight is the normal force we experience from the ground. In physics problems, when you are asked to determine apparent weight, the quickest method is usually to compute the normal force provided by the "ground".
One way to experience a reduced apparent weight is to strap into a harness of ropes and have someone (or some weight) pull down on the other end like they do in theater or films. Another way is to jump into a swimming pool, where the water lifts up on you. Another possibility, which we explore in this problem, is to enter an environment where the "ground" is capable of moving, such as an elevator.
Part A
Suppose a person with a weight of 686 N is in an elevator which is descending at a constant rate of 1.0 m/s and speeding up at a rate of 3.0 m/s2. What is the person's apparent weight?
Solution
System:
Interactions:
Model:
Approach:
Diagrammatic Representations
The physical picture and free body diagram for the person is:
|
|
Physical Picture |
Free Body Diagram |
|---|
Mathematical Representation
which leads to the form of Newton's 2nd Law for the y direction:
\begin
[ \sum F_
= N - mg = ma_
]\end
In our coordinates, the acceleration of the person is ay = -3.0 m/s2, giving:
\begin
[ N = ma_
+ mg = \mbox
]\end
Is the answer sensible?
This result for the normal force is less than the person's usual weight, in agreement with our expectation that the person should feel lighter while accelerating downward.
Part B
Suppose a person with a weight of 686 N is in an elevator which is ascending at a constant rate of 1.0 m/s and slowing down at a rate of 3.0 m/s2. What is the person's apparent weight?
Solution
System, Interactions and Model:
Approach:
Part C
Suppose a person with a weight of 686 N is in an elevator which is ascending at a constant rate of 1.0 m/s and speeding up at a rate of 3.0 m/s2. What is the person's apparent weight?
Solution
System, Interactions and Model:
Approach:
[Examples from Dynamics]