work

An interaction which produces a change in the mechanical energy of a system, or the integrated scalar product of force and displacement.

Motivation for Concept

It requires effort to alter the energy of an object, as can clearly be seen when attempting to impart kinetic energy by pushing a car which has stalled or to impart gravitational potential energy by lifting a heavy barbell. We would like to quantify what we mean by "effort". It is clear that force alone is not enough to impart energy. Suppose that the car or the barbell is just too heavy to move. Then, for all the pushing or pulling that is done (a considerable force), no energy is imparted. For the energy of a system to change, the system must alter its position or its configuration. In effect, the force must impart or reduce motion of the object to which it is applied.

Mathematical Definition

Work-Kinetic Energy Theorem as Postulate

Suppose that we postulate the Work-Kinetic Energy Theorem for a point particle as the defining relationship of work. Doing so will allow us to find a mathematical definition of work in terms of force.

Statement of the Theorem

If all the influences on a point particle are represented as works, the net work done by the forces produces a change in the kinetic energy of the particle according to:

Derivation of the Theorem

From Newton's 2nd Law for a point particle, we know

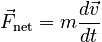
Now suppose that the particle undergoes an infinitesimal displacement dr. Since we want to bring the left side of the equation into line with the form of the expression for work, we take the dot product of each side with the displacement:

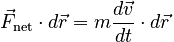
Before we can integrate, we make a substitution. Since v is the velocity of the particle, we can re-express the infinitesimal displacement as:

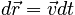
Making this substitution on the right hand side of the equation, we have:

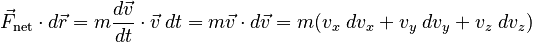
We can now integrate over the path:

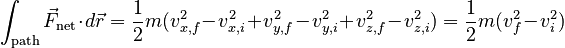
which is equivalent to the Work-Kinetic Energy Theorem.

Definition of Work

By comparing the derivation of the theorem to its statement, we see that in order for the theorem to be satisfied, we must make the definition:

which leads us to define the work done by an individual force as:

Importance of Path

Conservative Forces treated as Potential Energy

The form of our definition of work involves a path integral. For some forces, however, the value of the path integral is determined solely by its endpoints. Such forces are, by definition, conservative forces. This path-independence is the property which allows us to consistently define a potential energy to associate with the force. Thus, the work done by conservative forces will usually be ignored, since their interaction is instead expressed as a contribution to the mechanical energy of the system. The two commonly considered conservative forces in introductory mechanics are:

• gravitation (universal)
• spring forces

Non-Conservative Forces

Common forces in introductory physics whose effects are usually path dependent are:

• contact force
• normal force
• friction
• tension

For these forces, it is not possible to define a useful potential energy, and so the path of the system must be understood in order to compute the work when energy is used to describe a system subject to these interactions.

Example of Friction

To see the dependence of non-conservative work on path, consider a box of mass m moving along a rough, level surface. Suppose the box is subject only to horizontal applied forces, gravity, normal force and kinetic friction as it moves. Suppose the box is moved in one dimension from position x_i directly to position x_f as shown in the figure below.

Unable to render embedded object: File (work1stage.png) not found.

If we assume that the coefficient of kinetic friction is a constant μ_k, we can find an expression for the work done by friction in the course of this movement. The friction force will be:

where N is the normal force on the box from the floor. However, since the box is only moving horizontally (meaning a_y is zero) and the only vertical forces are gravity and the normal force, we can draw the free body diagram below.

Unable to render embedded object: File (workfbd.png) not found.

The diagram implies we can write Newton's 2nd Law for the y direction as:

This tells us that the normal force is equal in magnitude to the box's weight and so the force of friction has the constant magnitude:

Further, since friction is always opposite to the motion, and the motion is always in the + x direction, we can write:

and:

Thus, our path integral is reduced to a one-dimensional integral of the form:

which seems to depend only upon the endpoints. Consider, however, the alternate path between the same endpoints x_i and x_f shown here:

Unable to render embedded object: File (work3stage.png) not found.

This path has the box first making the trip from the position x_i to a position x_m between the initial and final positions of the box, then returning to the initial position x_i and then completing the trip to the final position x_f. Again, the box is assumed to be subject to purely horizontal applied forces, so that the friction force has a constant magnitude of:

To evaluate the path integral for the work, we must break the path up into three parts which consist of motion in one direction only. The parts coincide with the stages labeled 1 through 3 in the figure above. In each stage, we must determine the vector form of the friction force.

We can now write the path integral for the work, using the fact that all motion is in the x direction:

The result of the integrations is:

where d is the total distance (not displacement) traveled by the box. Since distance depends on the path (it is not a function of the endpoints only) we see that the exact path traveled by the box is important.

Relevant Examples