Consider a box of mass m moving along a rough, level surface. The box is subject only to horizontal applied forces, gravity, normal force and kinetic friction as it moves.
Part A
First, suppose the box is moved in one dimension from position xi directly to position xf as shown in the figure below.
Assuming that the coefficient of kinetic friction is a constant μk, find an expression for the work done by friction in the course of this movement.
Solution
System: Box as point particle.
Interactions: The box experiences external interactions with the earth (gravity), the surface (normal force and kinetic friction) and whatever is pushing it (applied force).
Model: Point Particle Dynamics plus the definition of work.
Approach:
Diagrammatic Representation
A free body diagram for the box will look like:
Mathematical Representation
The friction force will be:

where N is the normal force on the box from the floor. However, since the box is only moving horizontally (meaning ay is zero) the free body diagram implies we can write Newton's 2nd Law for the y direction as:

This tells us that the normal force is equal in magnitude to the box's weight and so the force of kinetic friction has the constant magnitude:

Further, since kinetic friction is always directed opposite to the motion, and the motion is always in the + x direction, we can write:

and:

Thus, our path integral is reduced to a one-dimensional integral of the form:

which depends only upon the endpoints...
Part B
Now consider the alternate path between the same endpoints xi and xf shown here:
What is the work done by kinetic friction on the box in the course of this movement?
Solution
System, Interactions and Model: As in Part A.
Approach:
Diagrammatic Representation
Stage 1 FBD |
Stage 2 FBD |
Stage 3 FBD |
|---|
Mathematical Representation
This path has the box first making the trip from the position xi to a position xm between the initial and final positions of the box, then returning to the initial position xi and then completing the trip to the final position xf. Just as in Part A, the box is assumed to be subject to purely horizontal applied forces so that the friction force has a constant magnitude of:
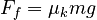
To evaluate the path integral for the work, we must break the path up into three parts which consist of motion in one direction only. The parts coincide with the stages labeled 1 through 3 in the figure above. In each stage, we must determine the vector form of the friction force.
The same splitting of the path is needed for the computation of the distance traveled in kinematics.

It is important to ensure that the friction force vector always points in the direction opposite the motion.
We can now write the path integral for the work, using the fact that all motion is in the x direction:

Note that although the box is moving in the --x direction in the middle part of the path integral, the differential dx remains positive. The sign of the motion is encoded in the endpoints of the integral. The lower limit of the integration is a larger x value than the upper limit, implying that the box is moving in the --x direction.
For a conservative force such as gravity, there would be no sign flip in the middle term, so that the sum of the first two integrals would be zero, and the integration would simply be from xi to xf, giving dependence only on the endpoints of the path.
The result of the integrations is:
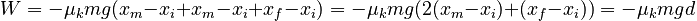
where d is the total distance (not displacement) traveled by the box. Since distance depends on the path (it is not a function of the endpoints only) we see that the exact path traveled by the box is important.



