null
Part A
A person pushes a box of mass 15 kg along a floor by applying a perfectly horizontal force F. The box accelerates horizontally at a rate of 2.0 m/s2. Assuming the coefficient of kinetic friction between the box and the ground is 0.45, what is the magnitude of F?
Solution
System:
Interactions:
Model:
Approach:
Diagrammatic Representation
The free body diagram for this situation is:
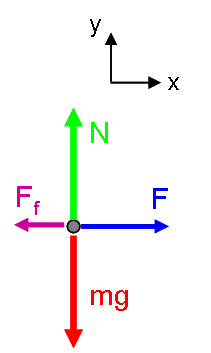
Mathematical Representation
With this free body diagram, Newton's 2nd Law can be written:
\begin
[ \sum F_
= F - F_
= ma_
]
[ \sum F_
= 0 ]\end
where we have assumed that the y acceleration is zero because the box is sliding along a horizontal floor, not moving upward or downward. This realization is important, because we know Ff = μN. Thus, because the y acceleration is zero, we can solve Newton's 2nd Law in the y direction to yield:
\begin
so that:
\begin
[ F = ma_
+F_
= ma_
+ \mu_
N = ma_
+ \mu_
mg = \mbox
] \end
Part B
A person pushes a box of mass 15 kg along a floor by applying a perfectly horizontal force F. The box moves horizontally at a constant speed of 2.0 m/s in the direction of the person's applied force. Assuming the coefficient of kinetic friction between the box and the ground is 0.45, what is the magnitude of F?
System, Interactions and Model:
Approach: