Top View |
Side View |
|---|---|
|
|
Suppose a soccer player is taking a corner kick. The 0.450 kg ball is launched at 45° from ground level and travels straight across the field (in the y direction in the diagram) until it is contacted by an attacking player's head at a height of 2.0 m above the ground 20.0 m horizontally from the point of the kick. After the header, the ball is traveling at the same speed as just before the header, but it is moving purely horizontally downfield (the x direction in the diagram).
Part A
What is the magniude of the impulse delivered to the player's head by the ball during the header? (Ignore the effects of air resistance for this estimate.)
Solution
System:
Ball as a point particle.
Interactions:
During its projectile motion toward the player, the ball is subject to an external influence from the earth(gravity). During the collision, we assume that the force from the player's head (contact force) is much larger than gravity.
Models:
Projectile Motion (One-Dimensional Motion with Constant Velocity in the y direction and One-Dimensional Motion with Constant Acceleration in the z direction) plus Momentum and External Force.
Approach:
An Important Clarification: Why consider the ball to be the system?
Although we are asked for the impulse acting on the player's head, it is simpler to calculate the impulse delivered to the ball by the player's head and then find the desired quantity using Newton's 3rd Law.
Phase 1: Projectile Motion
The problem has two parts. First, we use the methods of projectile motion to determine the velocity of the soccer ball immediately prior to the collision. Note that because this problem uses two horizontal coordinates, the projectile motion occurs in the yz plane, with gravity in the - z direction. Choosing the kick to originate from the point (0,0,0) at time t = 0, our givens are:
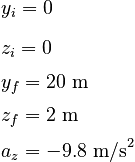
The most direct way to proceed is to express the time (which we do not need to solve for) in terms of the y-velocity:
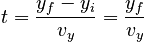
Then, we can substitute into the equation:
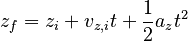
to obtain:
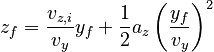
In this equation, we can use the fact that the launch angle is 45°, which tells us vz,i = vy, so:
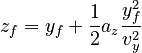
This equation is solved to obtain:
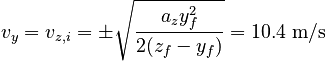
We choose the plus sign, since we have set up our coordinates such that the ball will move in the + y direction.
We are not finished, since we also need vz,f, the z-velocity at the end of the projectile motion and at the beginning of the ball's collision with the player's head. To find this velocity, we can use:
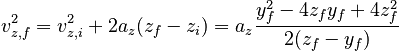
giving:
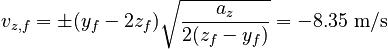
We choose the sign that makes vz,f negative, presuming that the ball is on the way down.
Can you prove to yourself that the minus sign is the only consistent choice when taking the square root above?
Phase 2: Collision
We have now completed the analysis of the projectile motion. Using the fact that the final velocity of the projectile motion will equal the initial velocity of the collision with the player's head, we summarize the initial velocity of the ball for the collision:
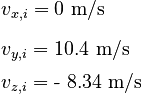
The magnitude of the initial velocity is then:
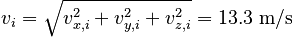
Thus, from the information given in the problem, we will take the final velocity of the ball immediately following the collision with the player's head to be:
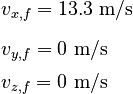
The impulse delivered to the ball during its contact with the player's head is therefore:
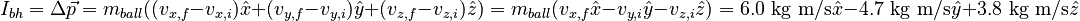
It is important to think carefully about the expected signs when calculating a change. The ball ends up with a positive x-momentum, so the x-impulse is positive. The ball loses a positive y-momentum, so the y-impulse is negative, the ball loses a negative z-momentum, so the z-impulse is positive.
Technically, we have not found Ibh, but rather the total impulse on the ball during the collision. If the collision is long enough, gravity's contribution to this impulse might be non-negligible. How much of a difference would be made in the result for Ibh by including the effects of gravity assuming a collision time of 0.050 s?
Note, however, that we were asked for the impulse delivered to the player's head. By Newton's 3rd Law, that impulse is simply:
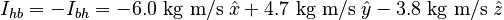
The magnitude of this impulse is 8.48 kg m/s.
Part B
Assuming a (generous) collision time of 50 ms, what is the average magnitude of the force imparted to the player's head by the ball during the collision?
Solution
System:
Player's head as a point particle.
Interactions:
We are only interested in the influence from the soccer ball (collision force).
Model:
Approach:

