The time integral of force. The net external impulse acting on a system over a given time interval is equal to the system's change in momentum.
Motivation for Concept
Although some everyday interactions like gravity and friction result in stable forces whose effects can easily be analyzed with dynamics, many interactions are not steady. Consider, for example, the difference between a push and a punch. When you push something, you consciously use your muscles to apply a steady force to the target object. For this reason, pushing a bowling ball or a bean bag feels much the same, apart from the fact that the bean bag will probably deform more in response to the force. When you punch something, however, you simply let your fist fly. The force felt by the target object and the reaction force exterted on your fist are the result of the impact of your moving fist with the object. This impact is essentially out of your control. The force exterted is not determined solely by your muscles (though the faster your fist is moving, the greater the force will tend to be), but rather it is principally determined by the properties of your hand and the target object. Because of this fact, there is a dramatic difference between the results of punching a bean bag versus punching a bowling ball.
Such impact or collision forces are extremely common in everyday life. Almost any sport will involve collisions. Household activities like hammering nails or kneading dough require collisions. Understanding collisions is also of great importance to car manufacturers.
Unfortunately, the forces during a collision are very difficult to characterize. They change extremely rapidly in time (the entire duration of a typical collision is measured in milliseconds), and they manner in which they change is strongly dependent on the material properties of the objects undergoing the collision. Because of these complications, it is rare to see a detailed force profile for a collision. Instead, collisions are usually described by an effect that is much more easily observed: the resulting change in the motion of the participants. The impulse delivered by a collision is one measure of this change.
Photos taken with a high-speed camera showing the impact of a tennis ball dropped from a height of 100 inches onto wood. |
Note that the center images are less blurry than the first and last. Can you explain this?
The ball rebounds because it is elastic. The deformation of the ball observed in the center image is not permanent. The ball's structure causes it to return to its initial shape, and in the process it pushes itself off the ground. If the ball were made of clay, the deformation would remain and the ball would simply "splat" onto the ground (one more example of how structural differences complicate collision analysis).
Definition of Net Impulse in terms of Momentum
Vector Change in Momentum
Suppose an object experiences a sudden interaction that results in a dramatic change in the object's momentum. One definition of the net impulse provided during the change in motion is to calculate the numerical value of the change in the object's momentum. In other words, the impulse J is:
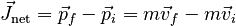
Note that because momentum is a vector, the change in momentum is also a vector. Thus, the impulse is by defintion a vector quantity. As with any vector quantity, it is important to remember that the calculation of impulse really involves three equations, one for each component:
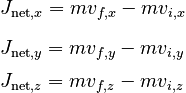
Initial-State Final-State Diagrams
The vector nature of momentum means that it very important when calculating the change to carefully set up a coordinate system. For this reason, it is strongly recommended that you begin any problem involving a change in momentum by constructing an intial-state final-state diagram.
Definition of Impulse in terms of Force
Impulse and Newton's Second Law
The integral form of Newton's 2nd Law states that:
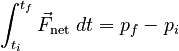
Comparing this with our first definition of impulse, it is obvious that we can also define the total impulse as:
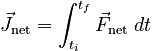
Inspired by this definition, we will sometimes refer to the impulse provided by a single force as:
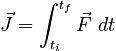
so that the net impulse acting on a system is:
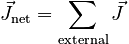
Impulses resulting from internal forces cancel by Newton's Third Law.
Time-Averaged Force
Since collision forces often have a complicated time evolution, it is rare for them to be easily integrable as a function of time. Thus, it is rare for the definition of impulse in terms of force to be used to find impulse. Instead, it is often used "in reverse" to characterize the forces involved in a collision. First, the change in impulse of the object involved in the collision is determined, then the impulse is used to estimate the force. Again, the detailed form of the force will be too complicated to find in this way, but if the total duration of the collision, Δt=tf - ti, is known, then it is possible to find the time-averaged net force experienced by the object during the collision. The time-averaged net force is, by definition:
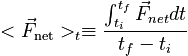
This definition makes it clear that the time-averaged net force is directly related to the net impulse:
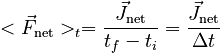
To see why different averages need not give the same value, consider two babysitters who each make $15 per hour. They have the same time-averaged income. Suppose, however, that one of the sitters gets jobs that last 3 hours on average, while the other's jobs are 4 hours. Their job-averaged income is different ($45 vs. $60). Similarly, you could imagine two people who mow lawns for extra income, charging $40 per lawn. Their job-averaged income is the same, but their time-averaged income could be different if they tend to mow different sized lawns.
Average Force and the Direction of Impulse
Remembering that the impulse is directly proportional to the average net force in a collision may help you to gain an intuitive understanding for the direction of the impulse in many problems. Because they are directly related, the net impulse must point in the same direction as the average net force.






1 Comment
David E Pritchard
I think the usual epistemology is to define Impulse as integral of force, then use N's law to deduce it's change of momentum. THe definition of average force should just be the impulse divided by \Delta t, which leads to the expression most often used to find the force when they are told the collision lasts 1.2 ms.
If the force in N's 2nd law is \Sum F^ext (which it should be) maybe we should introduce J^ext. I think going back to ^net suggests return to single particle dynamics.