MIT 8.01 Lesson 5: Motion with Constant Acceleration (Steady Net Force)
Lesson Summary
Learning Objectives
After completing this Lesson, students should be able to:
- understand and use the One-Dimensional Motion with Constant Acceleration model template from the [Model Hierarchy].
- accomplish the Learning Objectives listed in that template.
Stable Interactions Required
According to Newton's Laws of Motion, a system experiencing constant acceleration is necessarily experiencing a constant net interaction. Thus, this model can only be applied when the interactions are fairly steady. It is important to remember that a constant acceleration must have a constant direction as well as a constant size. Thus, if the forces on a system are clearly changing direction during the motion being analyzed, it is not reasonable to apply the One-Dimensional Motion with Constant Acceleration model.
An Abundance of Laws of Change
Integrating the definitions of acceleration and velocity for the special case that acceleration is constant leads to four expressions that are commonly encountered in descriptions of motion with constant acceleration:
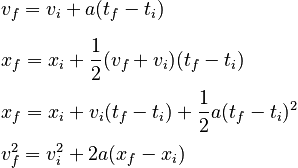
It is clear from these equations that there are seven possible unknowns in a given problem involving motion between two points with constant acceleration:
- initial time ( ti )
- final time ( tf )
- initial position ( xi )
- final position ( xf )
- initial velocity ( vi )
- final velocity ( vf )
- acceleration (constant) a
Remember that you will usually have the freedom to define the initial time and the initial position by setting up a coordinate system.
Looking at the four equations, you can see that each is specialized to deal with problems involving specific combinations of these unknowns.
Training Flight (In this example we will calculate acceleration, time, speed, and distance assuming constant acceleration.)
An Exercise in Derivation
Because the initial position and initial time can generally be arbitrarily chosen, it is often useful to rewrite all these equations in terms of only five variables by defining:
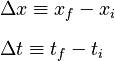
If you replace the initial and final positions and times with these "deltas", then each of the equations given above involves exactly four unknowns. Interestingly, the four equations represent all but one of the unique combinations of four variables chosen from five possible unknowns. Which unique combination is missing? Can you derive the appropriate "fifth equation"?
Graphical Representations
One way to graphically represent constant acceleration is to draw a velocity versus time graph. By the definition:
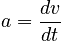
it is clear that the acceleration is equal to the slope of such a graph, so that if the acceleration is constant, the velocity versus time graph will necessarily be linear.
Another way to graphically represent acceleration is to note that the equation:
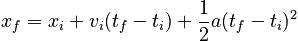
implies that for the case of constant acceleration, the position versus time graph describing the motion will be a parabola.
Decomposition of Complicated Motions
A wide variety of realistic one-dimensional motions can be closely approximated by decomposing the motion into segments of constant acceleration. By matching the initial conditions of each segment (time, position and velocity) to the final conditions of the previous segment, the entire motion can be described using only the simple Law of Change for the One-Dimensional Motion with Constant Acceleration model.
Accelerate, Decelerate (Determining the relationships between position, velocity and acceleration from a position vs. time plot.)
An Exercise in Continuity (Determining the relationships between position, velocity and acceleration from a position vs. time plot.)
Fan-Powered Ice Boat (Graphing 1D motion with constant acceleration.)
Decomposition of "Meeting" Problems into Multiple Systems
One common type of problem that often involves the One-Dimensional Motion with Constant Acceleration model has the goal of determining where two objects meet. Because this model can only describe the motion of a single particle, solving for the point at which two objects meet requires that the problem be approached by considering the two objects to be separate systems governed by separate models (or separate realizations of the same model). Finding the meeting point requires that appropriate constraints be applied to each system in order to ensure that their relative positions be accurate at the initial time and that they be equal at the meeting time.
Speed Trap (Police car with constant acceleration must catch speeder with constant velocity. )
Now that you have completed the Lesson, look at the model template for 1-D Motion with Constant Acceleration, which is intended to be a succinct summary of what you have learned.

