MIT 8.01 Lesson 3: Motion with Constant Velocity and Zero Net Force
Lesson Summary
We now explore our first model - motion with constant velocity. According to Newton, this is the natural state of motion that occurs when the net external force acting on a body is zero. This constant velocity will be measured with respect to any inertial coordinate system (but not an accelerating one).
Learning Objectives
After completing this Lesson, students should be able to:
- Describe the difference between distance and displacement.
- Define average velocity and average speed.
- Describe the features of a motion diagram that exhibits motion with constant velocity.
- Relate displacement, time and velocity.
- Find velocity from the slope of a position versus time graph.
- Describe the properties of the position versus time graph given the velocity and the initial position for a trip made at constant velocity.
- Mathematically determine when two objects moving with constant velocity will meet by constructing and solving a system of equations.
- Graphically determine when two objects moving with constant velocity will meet.
- understand and use the One-Dimensional Motion with Constant Velocity model template from the hierarchy of Models.
Allowed Systems and the Center of Mass
The concept of position can only (by definition) apply to a single point. Because of the central role of position in the One-Dimensional Motion with Constant Velocity model, the template for this model states that it is restricted to describe only a single point particle.
When an object is moving with constant velocity, however, the majority of the object will usually be moving with the same velocity. Consider, for example, a truck moving down the road at a constant speed. You could describe the position of the truck by any given point on the truck's frame: the driver's side door handle, the right front headlight, the rear license plate, etc. No matter which point you pick, you will find essentially the same motion, with a small offset of the absolute position. The velocity of any of these points is identical. Thus, even though a truck is certainly not a true point particle, it can be thought of as one for the purposes of this model. Further, essentially any point on the truck can be chosen as the location of the "point particle truck", but because later models will require us to think of the linear motion of a body as the motion of its center of mass it is advantageous to begin training ourselves now to think of the truck's center of mass as the appropriate point at which to label the truck's "true" position.
Relevant Interactions - All and None
The One-Dimensional Motion with Constant Velocity - Zero Net Force model applies when there is zero net force on an object. This does not mean there are no forces or interactions present - it means that if any interaction acts on the system it either produces a negligible force or its force is perfectly balanced by forces from opposing interactions. Thus, there are no interactions that are particularly relevant for the Law of Change for this model.
The Law of Change
Because of the extreme restrictions placed on the systems and interactions described by the One-Dimensional Motion with Constant Velocity model, the Law of Change for the model is rather simple. The mathematical definition of velocity (for one-dimensional motion) is:

If v is a constant, this equation can be straightforwardly integrated:

which (after algebraic rearrangement) gives:
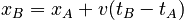
where:

It is rare for physics problems to specify an initial time for a motion, but rather they will usually specify an elapsed time. For instance, instead of saying "a car began a trip at 10:05 AM and drove until 10:15 AM", the problem will usually specify only that the car drove "for 10 minutes". Elapsed time is equivalent to the difference tB - tA.
Coordinate Systems
Because a difference in position is required when employing the Law of Change for the One-Dimensional Motion with Constant Velocity model, it is important to carefully consider the problem statement, define a useful coordinate system, and accurately assign the initial and final positions. The power to choose an advantagous origin and direction for your coordinates is a feature of all the motion models that can often be exploited to simplify calcuations, but it is important to remember that with great power comes great responsibility: failing to consciously choose a coordinate system can lead to sloppy math and an incorrect solution.
Overdriving Headlights (How long can you drive at constant velocity before you have to hit the brakes, assuming standard night detection distances?)
Graphical Representation
The Law of Change for the One-Dimensional Motion with Constant Velocity model can be expressed:

which is remeniscent of the equation for the slope of a line. In fact, if we plot a position versus time graph, then the equation above becomes exactly the equation for the slope of the graph. Since we know that v is constant, the slope is constant and the graph will be a line.
A Velocity for Words (Put the motion described by these graphs into words.)
Decomposition of Complicated Motions
Although it is rare on earth for an object to move continuously with constant velocity, many realistic motions can be decomposed into segments that are well represented by constant velocity motion. By matching the initial conditions of each segment (time and position) to the final conditions of the previous segment, the entire motion can be described using only the simple Law of Change for the One-Dimensional Motion with Constant Velocity model.
Campus Tour (Basic problem to illustrate graphical representation of position and velocity.)
Decomposition of "Meeting" Problems into Multiple Systems
One common type of problem that often involves the One-Dimensional Motion with Constant Velocity model has the goal of determining where two objects meet. Because this model can only describe the motion of a single particle, solving for the point at which two objects meet requires that the model be applied twice considering the two objects to be separate systems. Finding the meeting point requires that appropriate constraints be applied to each system in order to ensure that their relative positions be accurate at the initial time and that they be equal at the meeting time.
Where Do We Meet? (Two people moving in one dimension with constant speed are destined to meet – but where?)
Now that you have completed the Lesson, look at the model template for 1-D Motion with Constant Velocity, which is intended to be a succinct summary of what you have learned.

