Down the Ramp

Consider a ball placed on a ramp inclined at θ = 30° above the horizontal.

Part A

What is the acceleration of the ball's center of mass as it rolls down the ramp? Assume that the ball rolls without slipping.

Solution

We consider two methods.

Method 1: Dynamics

System:

The ball is treated as a rigid body.

Interactions:

External influences from the earth (gravity) and the ramp (friction and normal force).

Model:

Single-Axis Rotation of a Rigid Body plus Point Particle Dynamics

Approach:

Diagrammatic Representation

The ball will translate and rotate as it rolls down the slope. The relevant free body diagram is shown below.

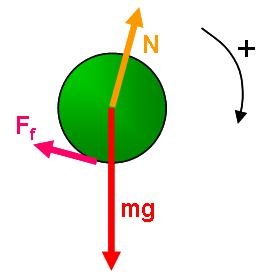
Mathematical Representation

From this free body diagram we can construct Newton's 2nd Law for the ball's center of mass and also the angular version of Newton's 2nd Law for rotations of the ball about the center of mass. The x-component of Newton's 2nd Law is:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[\sum F_

Unknown macro: {x}

= mg \sin\theta - F_

Unknown macro: {f}

= ma_

] \end

and the sum of torques about the center of mass is:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \sum \tau = RF_

Unknown macro: {f}

= I\alpha ] \end

It is not appropriate to assume that the friction force is equal to μF_N. The ball is moving, but the point of contact with the ground will remain stationary, and hence we are in the static friction regime.

We can eliminate the friction force from the two equations to find:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ mg \sin \theta = ma_

Unknown macro: {x}

+ I\frac

Unknown macro: {alpha}

Unknown macro: {R}

] \end

Now, because the ball is rolling without slipping, we can relate the angular acceleration to the linear acceleration of the center of mass:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \alpha R = a_

Unknown macro: {x}

] \end

Substituting this expression allows us to express the acceleration as:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ a = \frac

Unknown macro: {g sintheta}

{1 + \frac

Unknown macro: {displaystyle I}

{\displaystyle mR^

Unknown macro: {2}

}} ]\end

Using the result that the moment of inertia for a sphere is 2/5 m R², we have:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ a =\frac

Unknown macro: {g sintheta}

{1+\frac

Unknown macro: {displaystyle 2}

{\displaystyle 5}} = \frac{5 g \sin(30^

Unknown macro: {circ}

)}

Unknown macro: {7}

= \mbox

Unknown macro: {3.5 m/s}

]\end

Note that we have been given no information whatever about the mass or radius of the ball! The acceleration is independent of the mass and the radius.

Method 2: Angular Momentum

System: The ball as a rigid body.

Interactions:

External influences from the earth (gravity) and the ramp (normal force and friction).

Model:

Angular Momentum and External Torque about a Single Axis.

Approach:

Diagrammatic Representation

Instead of writing separate Laws for the translation and rotation, we could instead choose to simply consider the movement as angular momentum about a fixed axis. Since the friction force is unknown, it is best to choose an axis on the surface of the ramp such as the one shown in the picture below.

Mathematical Represenation

The torques about this axis will depend upon the position of the ball. When the ball has moved a distance x along the ramp, the torques from gravity and the normal force will be:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[\sum \tau = mg(x\cos\theta+R \sin \theta) - Nx ] \end

The expression for the torque due to the ball's weight is most easily found using the lever arm.

But, using the fact that the ball is not tranlating in the y-direction, we can derive the standard inclined plane relation:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ N = mg\cos\theta]\end

which gives:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \sum \tau = mgR \sin \theta ] \end

We must now find an expression for the angular momentum of the ball. Even though we have not chosen to write separate dynamical equations for the rotation about the center of mass and the translation, the ball's angular momentum will still be composed of these two parts:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ L = I_

Unknown macro: {rm cm}

\omega_

+ \vec

Unknown macro: {r}

_

Unknown macro: {rm cm,axis}

\times m \vec

Unknown macro: {v}

_

Unknown macro: {rm cm}

= I_

\omega_

Unknown macro: {rm cm}

+ m v_

R ]\end

Because the ball rolls without slipping, we can relate the angular speed about the center of mass axis to the translational speed of the center of mass:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \omega_

Unknown macro: {rm cm}

R = v_

] \end

Substituting gives:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ L = I_

Unknown macro: {rm cm}

\frac{v_{\rm cm}}

Unknown macro: {R}

+ mv_

R ] \end

We now set the time derivative of the angular momentum equal to the sum of the torques, giving:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \left(\frac{I_{\rm cm}}

Unknown macro: {R}

+ mR\right)a = mgR\sin\theta ] \end

so that we find:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ a = \frac

Unknown macro: {gsintheta}

{1 + \frac

Unknown macro: {displaystyle I}

{\displaystyle mR^

Unknown macro: {2}

}} ] \end

deck: com.atlassian.confluence.macro.MacroExecutionException: java.lang.NullPointerException

Part B

Assuming the ball is released from rest, what is the speed of the ball's center of mass after it has moved 1.3 m along the ramp?

Solution

Once again, we solve the problem using two different methods.

Method 1: Kinematics

System, Interactions and Models: As in Part A, plus One-Dimensional Motion with Constant Acceleration.

Approach:

Method 2: Energy

System:

The ball plus the earth and ramp.

Interactions:

There are internal gravity, normal and friction forces. Gravity is conservative, while the normal force and friction are non-conservative.

Model:

Mechanical Energy, External Work, and Internal Non-Conservative Work.

Approach:

Another way to solve the problem is to use energy. It turns out that in this problem, the mechanical energy of the ball will be constant. This assertion requires justification. The forces present in the system are gravity, normal force and friction. Gravity is a conservative force. The normal force is non-conservative, but it does no work because it is perpendicular to the motion of the object. Friction, however, is both non-conservative and directed anti-parallel to the motion of the ball, and so it should clearly do work. The reason we can assume the energy is constant is the problem's statement that the ball rolls without slipping. This means that the friction is static rather than kinetic. Kinetic friction converts mechanical energy into thermal energy and so it is not appropriate to use conservation of mechanical energy when kinetic friction is present. The work done by static friction, however, does not convert mechanical energy into thermal energy. Instead, the static friction acts to divert some of the lost potential energy into rotational kinetic energy (rather than simply translational kinetic energy). Thus, all of the energy remains in a mechanical form.

With this realization, we can write the equation of mechanical energy conservation in the form:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ K_

Unknown macro: {rm f}

+ K_

Unknown macro: {rm rot,f}

+ U_

Unknown macro: {rm g,f}

= K_

Unknown macro: {rm i}

+ K_

Unknown macro: {rm rot,i}

+ U_

Unknown macro: {rm g,i}

]\end

If we select h = 0 at the point of release of the ball, then by the time the ball has moved a distance x along the ramp, it has reached a height:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ h = - x \sin\theta]\end

Substituting zeros and appropriate expressions into the conservation of energy formula gives:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \frac

Unknown macro: {1}

Unknown macro: {2}

mv_

Unknown macro: {f}

^

+ \frac

Unknown macro: {2}

I\omega_

Unknown macro: {f}

^

- mgx\sin\theta = 0 ] \end

Finally, the assumption that the ball is rolling without slipping implies the relationship:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \omega_

Unknown macro: {f}

R = v_

]\end

so:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ v_

Unknown macro: {f}

= \sqrt{\frac

Unknown macro: {2gxsintheta}

{1+\frac

Unknown macro: {displaystyle I}

{\displaystyle mR^{2}}}} ] \end

The same result as obtained with method 1.

Looking back at the equations of Part A, method 1 you can see that the friction force is:

Unknown macro: {latex}

[ F_

Unknown macro: {f}

= I\alpha /R ]

We know the value of α from Part A. Thus, using the fact that the work done by friction when the ball moves a distance x down the ramp is W = – xF_f we can write:

Unknown macro: {latex}

[ W = - \frac

Unknown macro: {xI}

{R^{2}} \frac

Unknown macro: {gsintheta}

{1+\frac

Unknown macro: {displaystyle I}

{\displaystyle mR^

Unknown macro: {2}

}} ]

Now, using our result for v_f, we can write this as:

Unknown macro: {latex}

[ W = - \frac

Unknown macro: {1}

Unknown macro: {2}

I \frac{v_

Unknown macro: {f}

^{2}}{R{2}} = - \frac

Unknown macro: {2}

I\omega_

Unknown macro: {f}

^

= - K_

Unknown macro: {rm rot}

]

Thus, the work done by friction is exactly equal to the rotational kinetic energy acquired by the ball.

Error rendering macro 'deck'

java.lang.NullPointerException

Error rendering macro 'deck'

java.lang.NullPointerException

html: Security restricted macro is not allowed. An edit restriction is required that matches the macro authorization list.

Child pages

Down the Ramp

Part A

Solution

Method 1: Dynamics

Method 2: Angular Momentum

Part B

Solution

Method 1: Kinematics

Method 2: Energy