Yun Yea-Ji (KOR) at the 2009 South Korean Figure Skating Championships
Photo courtesy Wikimedia Commons

Consider an ice skater performing a spin. The ice is very nearly a frictionless surface

A skater spinning around has constant angular momentum, but can change his or her Moment of Inertia by changing body position. What happens to their rate of rotation when they do so?

    Part A

    Assume that the skater originally is standing straight up while spinning, with arms extended. He or she then draws his or her arms inwards tightly to the sides. How does the angular velocity change?

    Solution

    System:

    The skater is treated as a rigid body in two configurations – one with the arms extended, the other with arms held close.

    Interactions:

    External influences – none. The skater is moving on a frictionless surface.

    Model:

    Single-Axis Rotation of a Rigid Body

    Approach:

    Diagrammatic Representation

    Consider the skater intially as a massless vertical pole with the arms modeled as massless rods of length Li with a point mass m at each end.

    After contracting the skater's arms, the two masses are each a distance Lf from the body

    Mathematical Representation

    The definition of the Moment of Inertia is:

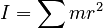
    So that if we calculate the initial Moment of Inertia about the vertical pole that is the skater's torso, we get:

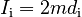
    For the "final" configuration the Moment of Inertia becomes:

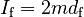
    The Angular Momentum L has a magnitude given by

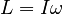
    so the initial angular momentum is

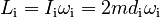
    and the final angular momentum is

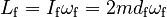
    Since the Angular Momentum is unchanged, the initial and final expressions should be equal. This means that

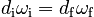
    or

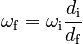
    After drawing in his or her arms, the skater is spinning much more rapidly, without the application of any external forces or torques.


    Part B

    Solution

    What if we address this from the standpoint of Energy? If the Energy is conserved (since there is no external work done on the system), then we ought to be able to derive the angular velocity from Conservation of Energy.

    This assumption really is not correct – Energy is NOT conserved in this case, despite the absence of outside forces. But we'll proceed to see where this assuimption leads.

    From our expressions for Rotational Energy, we know that the energy is given by

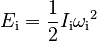
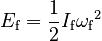
    If the energy is the same at the end as at the beginning, then we can equate these expressions. After some algebra, we get:

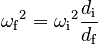
    The above equation is NOT correct.

    Clearly there is an error, since this does not agree with our previous result.

    The error is the assumption that energy is conserved. In drawing his or her arms inwards, the skater must exert force to bring them closer tto the axis and rotate faster. This force acting over a distance performs work and increases the system energy. The change in energy is given by the difference between the above expressions

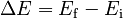
    Substituting in from the equations in Part A, one finds, after a little algebra:

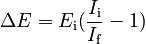
    If it is not clear how the Kinetic Energy can change within a closed system with no external torques or forces, see the example Rotating a Space Ship

    Error rendering macro 'deck'

    java.lang.NullPointerException

    html: Security restricted macro is not allowed. An edit restriction is required that matches the macro authorization list.

    <script type="text/javascript">
    var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
    document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
    </script>
    <script type="text/javascript">
    try {
    var pageTracker = _gat._getTracker("UA-11762009-2");
    pageTracker._trackPageview();
    } catch(err) {}</script>