Introduction
The Osiris engine is a liquid bipropellant rocket engine featuring active throttle control and thrust vectoring, designed for the Collegiate Propulsive Lander Challenge (CPLC). It uses isopropanol (IPA) as fuel and nitrous oxide (N₂O) as oxidizer. The engine is engineered to meet the following key performance specifications:
Mixture Ratio: 2.75
Burn Time: ~14 seconds at full throttle
Throttle Range: 32–100%
Chamber Material: GrCop-42
Total Impulse: 38,754 N·s
To ensure Osiris can reliably meet these requirements, a thorough design and analysis cycle is required. This page documents the process used by the MIT Rocket Team to design the Osiris engine to a level suitable for passing a Critical Design Review (CDR).
Nozzle Geometry
Fuel Inlet Manifold
Cooling Channels
A critical aspect of rocket engine design is determining how the combustion chamber will be cooled. Temperatures inside a high-performance rocket engine can reach over 6000°F (≈3315°C)—hotter than molten lava! At these temperatures, proper material selection, structural analysis, and cooling-geometry design become essential to ensuring engine survivability. Although many cooling methods exist, the final Osiris engine design uses a regeneratively cooled chamber featuring 40 cooling channels running along the chamber wall. These channels allow propellants (fuel or oxidizer) to absorb heat from the chamber before being injected into the combustion zone, improving both thermal management and overall engine efficiency. The following sections outline the process used to develop this cooling-channel geometry, including the structural and thermal analyses performed, the CEA/RPA performance modeling, and the iterative FEA workflow used to verify the design.
Initial Design (RPA)
Rocket Propulsion Analysis (RPA) was used for initial thermal and geometrical characterizations of the chamber. RPA takes performance parameters for the engine along with the geometry of the regenerative cooling channels, the mass flow of fuel through the channels, the thermal conductivity of the chamber material, and the mass flow dedicated to film cooling the chamber. For this project, the Bartz equation was selected as it provides a conservative estimate for the cooling performance. RPA then uses the bartz calculates the temperature distribution
Structural Analysis
To verify that the designed chamber can withstand operational conditions, it is essential to ensure that the cooling channels provide sufficient heat removal to prevent permanent damage to the chamber walls. During engine operation, the chamber is subjected to extremely high internal heat fluxes and pressures, which can result in significant thermal gradients, mechanical stresses, and deformation. If not properly analyzed, these effects can lead to excessive strain, local buckling, or other unwanted structural failures.
GrCop-42 was selected as the chamber material for several key reasons. As a copper alloy, it offers high thermal conductivity, which is essential for removing heat through regenerative cooling. Compared to pure copper, GrCop-42 provides significantly higher strength, particularly at elevated temperatures, making it far more suitable for the extreme thermal and mechanical loads experienced during engine operation. Although its thermal conductivity is slightly lower than that of pure copper, the substantial improvement in high-temperature strength more than offsets this difference for rocket applications. Notably, GrCop-42 was developed by NASA specifically for additively manufactured rocket engine components, making it an ideal choice for the Osiris chamber. Specifically, it is designed to be resistant to creep and cycle fatigue, which is ideal for our goals of firing the engine 10+ times. This paper goes deeper into the structural characteristics of GrCop-42.
Finding text and articles on how to analyze the stress incurred in the cooling channels was difficult. Initially, we settled on an equation found in this textbook, on page 207. Here, they use the following equation (for definitions for each variable, refer to the textbook):
| \sigma_t=\frac{p_l-\,p_g}{2} \left(\frac{w}{t_w}\right)^2 + \frac{E a \dot{q}t_w}{2(1 - \nu) k} |
The left term signifies the mechanical stress felt due to the pressure difference between the hot gas wall and the inner cooling walls. The right term signifies the thermal stress incurred due to the intense heat flux. With this in mind, we took the combination of the chamber geometry given from RPA (such as w,t_w) and the provided data for material constants (such as E, \nu, \alpha) and created a script that would analyze what \sigma_t for a given p_l, \dot{q}, which are both the main outputs we are concerned with from RPA, as detailed in the previous section.
As an aside, it is important to note that several material properties vary significantly with temperature. For our analysis, the key temperature-dependent properties are thermal conductivity k, Young’s modulus E, and the coefficient of thermal expansion \alpha. This requires taking the hot-gas-side wall temperature output from RPA and determining the corresponding material property values at that temperature.
However, two challenges arise:
Limited data availability: There is very little published temperature-dependent property data for GRCop-42.
Data format: Even when data exists, it is almost always presented as plots rather than in a machine-readable format such as CSV.
To address the first issue, we used the thermal-conductivity-versus-temperature curve for GRCop-42 from the previously referenced paper. For Young’s modulus and the coefficient of thermal expansion, we used published temperature-dependent curves for pure copper. This approach provides a conservative estimate of the stresses, since GRCop-42 generally has a slightly higher Young’s modulus and a slightly lower coefficient of thermal expansion than pure copper. Because GRCop-42 is also stronger than copper at high temperature, using copper-based property curves gives a reasonable—and conservative—approximation. To solve the second issue, we used a web digitizer, a tool that extracts numerical data points from plot images. The digitized data can then be exported as a CSV file and directly used in our calculations. A practical tip when digitizing is to place fewer points in regions where the curve is nearly linear and more points in regions with high curvature to preserve accuracy. A reliable web-based digitizer we used is linked here.
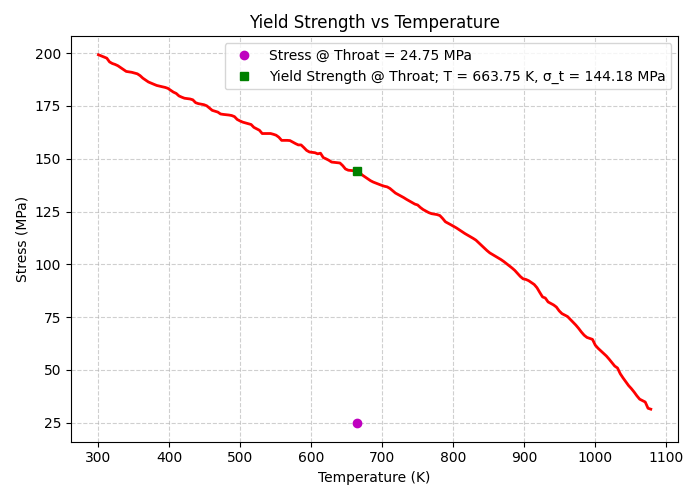
With the temperature-dependent data prepared, we next calculated the total stress ( \sigma_t) at the chamber throat. Initial test calculations showed that thermal stress dominated the total stress budget—often by nearly an order of magnitude compared to mechanical stress. Since RPA identifies the throat as the region experiencing the highest heat flux, this location represents the worst-case thermal loading. The logic follows that if the total stress at the throat remains below the material’s yield strength at that temperature, then the remainder of the chamber—experiencing lower thermal loads—will also remain structurally safe. The figure below shows the web-digitized plot of GRCop-42 yield strength versus temperature, the interpolated yield strength at the throat temperature, and the corresponding total stress we calculated at that temperature.
This calculation resulted in a factor of safety (FOS) of approximately 5.83, which would only increase during throttled operation. At first glance this seems ideal—however, an FOS this large immediately suggested that something in our assumptions was incorrect. After extensive research and a series of FEA simulations (the latter of which will be discussed in detail in a later section), we discovered the issue: our analytical model treated the cooling channels as an isolated thin ring in vacuum and applied a basic hoop-stress formulation. The figure below illustrates the physical scenario that this simplified equation actually represents:
[figure placeholder]
In reality, several important structural effects were being neglected, the most significant being the presence of the outer wall of the cooling channels, i.e., the cooling jacket. The cooling jacket constrains the thermal expansion of the inner channel walls. As heat flows in from the hot-gas wall, the channels attempt to expand outward, but the jacket restricts this motion. This interaction induces additional thermal and mechanical stresses in the channel walls—far larger than the simple ring stress predicted by the hand calculation.
In conclusion, while these hand calculations are useful for developing intuition about GRCop-42’s material behavior and confirming that basic hoop stresses are small, they are not sufficient to accurately predict the true stress state within the chamber. The only reliable way to evaluate total stress, strain, deformation, and overall survivability is through full FEA analysis using software such as SolidWorks or other high-fidelity structural solvers.