You are viewing an old version of this page. View the current version.
Compare with Current
View Page History
« Previous
Version 16
Next »
Unknown macro: {table}
Unknown macro: {tr}
Unknown macro: {td} [Examples from Momentum]
Unknown macro: {tr}
Unknown macro: {td}
The root page Examples from Momentum could not be found in space Modeling Applied to Problem Solving.
Unknown macro: {search-box}
A 4460 lb Ford Explorer traveling 35 mph has a head on collision with a 2750 lb Toyota Corolla, also traveling 35 mph.
Part A
Assuming that the automobiles become locked together during the collision, what is the speed of the combined mass immediately after the collision?
Solutions
System: Explorer plus Corolla as point particles.
Interactions: Impulse resulting from external influences will be neglected, as we assume that the collision is instantaneous.
Model: Momentum and External Force.
Approach:
Diagrammatic Representation
We begin by sketching the situation and defining a coordinate system.
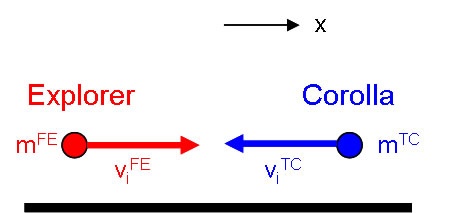
|
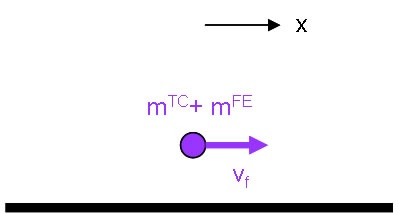
|
Initial State |
Final State |
Mathematical Representation
Since we assume that external forces are negligible during the collision, we set the external impulse to zero which gives:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ p^
Unknown macro: {TC}
_
Unknown macro: {x,i}
+ p^
Unknown macro: {FE}
_
= p^
Unknown macro: {system}
_
Unknown macro: {x,f}
]\end
or, in terms of the masses:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ m^
Unknown macro: {TC} v^
_
Unknown macro: {x,i}
+ m^
Unknown macro: {FE} v^
_
= (m^
Unknown macro: {TC}
+m^
Unknown macro: {FE}
)v_
Unknown macro: {x,f}
]\end
which gives:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ v_
Unknown macro: {x,f}
= \frac{m^
Unknown macro: {TC} v^
_
Unknown macro: {x,i}
+ m^
Unknown macro: {FE} v^
_{x,i}}{m^
Unknown macro: {TC}
+m^{FE}} = \mbox
Unknown macro: {3.71 m/s}
= \mbox
Unknown macro: {8.3 mph}
]\end
Part B
Find the impulse that acted on each of the vehicles during the collision.
Solution
Systems: Corolla and Explorer as separate point particle systems.
Interactions: The impulse on each vehicle from the other is assumed to be the dominant interaction during the collision. Because we are now considering the vehicles separately, these are now external impulses.
Model: Momentum and External Force.
Approach:
With the results of Part A it is straightforward to calculate the impulse on the Explorer due to the collision. To be specific, we label the impulse "EC" to remind ourselves the impulse on the Explorer is provided by the Corolla.
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ I^
Unknown macro: {EC}
_
Unknown macro: {x}
= p^
Unknown macro: {E}
_
Unknown macro: {x,f}
-p^
_
Unknown macro: {x,i}
= m^
Unknown macro: {E} (v^
_
Unknown macro: {x,f}
-v^
Unknown macro: {E}
_
) = (\mbox
Unknown macro: {2030 kg}
)(\mbox
Unknown macro: {3.71 m/s}
-\mbox
Unknown macro: {15.6 m/s}
) = -\mbox
Unknown macro: {24000 kg m/s}
] \end
Similarly, for the Corolla:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ I^
Unknown macro: {CE}
_
Unknown macro: {x}
= p^
Unknown macro: {C}
_
Unknown macro: {x,f}
-p^
_
Unknown macro: {x,i}
= m^
Unknown macro: {C} (v^
_
Unknown macro: {x,f}
-v^
Unknown macro: {C}
_
) = (\mbox
Unknown macro: {1250 kg}
)(\mbox
Unknown macro: {3.71 m/s}
+\mbox
Unknown macro: {15.6 m/s}
) = +\mbox
Unknown macro: {24000 kg m/s}
] \end
Part C
Assuming the collision lasted for 0.060 seconds, find the average force exerted on each vehicle.
Solution
Systems: Corolla and Explorer as separate point particle systems.
Interactions: The external force on each vehicle from the other is assumed to be the dominant interaction during the collision.
Model: Momentum and External Force.
Approach:
From the Law of Interaction, we know:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ I^
Unknown macro: {EC}
_
Unknown macro: {x}
= \int F^
_
Unknown macro: {x}
\:dt \equiv \bar
Unknown macro: {F}
^
Unknown macro: {EC}
_
\Delta t]\end
so the average force exerted on the Explorer is:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[\bar
Unknown macro: {F}
^
Unknown macro: {EC}
_
Unknown macro: {x}
= \frac{I^
Unknown macro: {CE}
_{x}}
Unknown macro: {Delta t}
= -\mbox
Unknown macro: {400,000 N}
]\end
Similarly, the average force exerted on the Corolla is:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[\bar
Unknown macro: {F}
^
Unknown macro: {CE}
_
Unknown macro: {x}
= \frac{I^
Unknown macro: {EC}
_{x}}
Unknown macro: {Delta t}
= \mbox
Unknown macro: {400,000 N}
]\end
Part D
Suppose a 75 kg person in each vehicle underwent the same change in velocity as their automobile in the same amount of time. Find the average force exerted on these people.
Systems: First, the Corolla and Explorer as separate point particle systems, then the passengers as separate point particle systems.
Interactions: Each vehicle is subject to a collision force from the other. The passengers are each subject to some decelerating force, possibly a seatbelt or airbag.
Model: Point Particle Dynamics.
Approach:
The passengers clearly are not subject to the same force as their vehicles. Rather, they are subject to the same accelerations. They are (hopefully) strapped into their automobiles, so that whatever happens to their vehicle happens to them as well. Thus, our first goal is to determine the vehicles' accelerations. This is easily accomplished using the results of Part C in Newton's 2nd Law.
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ a^
Unknown macro: {E}
_
Unknown macro: {x}
= \frac{F^
Unknown macro: {EC}
_{x}}{m^{E}} = -\mbox
Unknown macro: {200 m/s}
^
Unknown macro: {2}
]
[ a^
Unknown macro: {C}
_
= \frac{F^
Unknown macro: {CE}
_{x}}{m^{C}} = \mbox
Unknown macro: {320 m/s}
^
Unknown macro: {2}
]\end
With these accelerations, we can find the force on each driver:
Unknown macro: {latex}
\begin
Unknown macro: {large}
[ F^
Unknown macro: {E,driver}
_
Unknown macro: {x}
= m^
Unknown macro: {driver}
a^
Unknown macro: {E}
_
= -\mbox
Unknown macro: {15000 N}
= -\mbox
Unknown macro: {3,300 lbs}
]
[ F^
Unknown macro: {C,driver}
_
Unknown macro: {x}
= m^
Unknown macro: {driver}
a^
Unknown macro: {C}
_
= \mbox
Unknown macro: {24000 N}
= \mbox
Unknown macro: {5,400 lbs}
]\end

