Down the Well

A bucket for collecting water from a well is suspended by a rope which is wound around a pulley. The empty bucket has a mass of 2.0 kg, and the pulley is essentially a uniform cylinder of mass 3.0 kg on a frictionless axle. Suppose a person drops the bucket (from rest) into the well.

Part A

What is the bucket's acceleration as it falls?

Solution

We will consider two different methods to obtain the solution.

Systems:

The pulley and the bucket are treated as separate objects. The bucket can be treated as a point particle, but the pulley must be treated as a rigid body.

Interactions:

The pulley and the bucket are each subject to external influences from the rope and from Gravitation. The pulley is also subject to a force from the axle.

Model:

Rotation and Translation of a Rigid Body and Point Particle Dynamics

Approach:

Diagrammatic Representation

We begin with free body diagrams for the two objects.

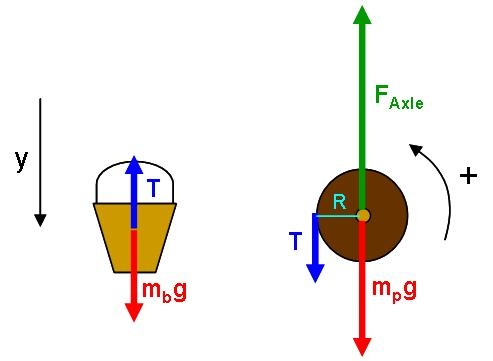
Note that the two forces acting on the bucket each have zero moment arm relative to the center of mass of the bucket. Thus, they have no tendency to produce rotation about the center of mass and so we can justifiably treat the bucket as a point particle.

Mathematical Representation

For the bucket, we write Newton's 2nd Law:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ m_

Unknown macro: {b}

g - T = m_

a_

Unknown macro: {b}

] \end

For the pulley, there will be no translation, only rotation about the center of mass. We sum the [torques] about the fixed axis defined by the axle:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ TR = I_

Unknown macro: {p}

\alpha_

] \end

We now make the assumption that the rope does not stretch or slip as it unwinds. These assumptions allow us to relate the rotation rate of the pulley to the motion of the bucket:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \alpha_

Unknown macro: {p}

R = a_

Unknown macro: {b}

]\end

With this assumption, we can solve the system of equations to obtain:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ a_

Unknown macro: {b}

= \frac

Unknown macro: {g}

{1+\frac{\displaystyle I_{p}}{\displaystyle m_

R^

Unknown macro: {2}

}} ] \end

Note that I_p/(m_bR²) is not equal to 1/2. The ratio of the pulley's moment of intertia to the pulley's mass times radius squared is 1/2, but we have the ratio of the pulley's moment of inertia to the bucket's mass times the pulley's radius squared.

or, using the formula for the moment of inertia of a cylinder:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ a_

Unknown macro: {b}

= \frac

Unknown macro: {g}

{1+\frac{\displaystyle m_{p}}{\displaystyle 2m_

}} = \mbox

Unknown macro: {5.6 m/s}

^

Unknown macro: {2}

]\end

As expected, the acceleration approaches g if the mass of the bucket goes to infinity, and it approaches zero if the mass of the pulley goes to infinity.

System: An alternate approach is to combine the bucket and the pulley into a single system.

Interactions:

The system is subject to external forces from the earth acting on the bucket and the pulley and from the normal force acting on the pulley.

Model:

1-D Angular Momentum and Torque

Approach:

Error rendering macro 'deck'

java.lang.NullPointerException

Part B

What is the bucket's speed after falling 5.0 m down the well?

Solution

Again, we will use two methods.

Method 1

System:

Bucket as point particle.

Interactins:

External influences from the earth (gravity) and the rope (tension).

Model:

One-Dimensional Motion with Constant Acceleration.

Approach:

Method 2

System:

Treat the bucket, pulley and the earth as a single system.

Interactions:

Internal interactions of gravity (conservative) and tension from the rope (non-conservative) plus an external influence from the normal force on the pulley (non-conservative).

Model:

Mechanical Energy and Non-Conservative Work.

Approach:

There will be no net non-conservative work on this system, even though there are non-conservative forces present. The normal force is a non-conservative external force, but does no work since the pulley experiences no displacement and the normal force has no moment arm and so exerts no torque. The tension forces on the pulley and the block are non-conservative internal forces. The tension forces do perform work on the system, but the work done by the downward tension on the pulley and the upward tension on the block are equal in size and opposite in sign. Therefore, their contributions cancel each other to give zero net non-conservative work.

To see that the net work from tension is zero requires us to use two methods of calculating work. Using force and displacement, you can show that the work done on the bucket is

Unknown macro: {latex}

[

Unknown macro: {W}

_

Unknown macro: {b}

= - |Ty|]

where |y| is the distance fallen. To find the work done on the pulley, we must use

Unknown macro: {latex}

[ W_

Unknown macro: {p}

= \tau (\theta - \theta_

Unknown macro: {i}

)]

but since

Unknown macro: {latex}

[ \tau = |T|R ]

and (assuming the rope does not slip or stretch)

Unknown macro: {latex}

[ \theta - \theta_

Unknown macro: {i}

= |y|/R ]

we find that

Unknown macro: {latex}

[ W_

Unknown macro: {p}

= + |Ty| ]

.

We can now use the conservation of energy, which consists of three parts:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ K_

Unknown macro: {rm trans,i}

+ K_

Unknown macro: {rm rot,i}

+ U_

Unknown macro: {rm g,i}

= K_

Unknown macro: {rm trans,f}

+ K_

Unknown macro: {rm rot,f}

+ U_

Unknown macro: {rm g,f}

] \end

If we set h= 0 to be at the initial position of the bucket, then we can write:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ m_

Unknown macro: {p}

g(-y_

Unknown macro: {a}

) = \frac

Unknown macro: {1}

Unknown macro: {2}

m_

Unknown macro: {b}

v_

^

+ \frac

Unknown macro: {2}

I_

\omega_

Unknown macro: {p}

^

Unknown macro: {2}

+ m_

Unknown macro: {b}

g(-y_

) + m_

g(-y_

Unknown macro: {a}

) ] \end

Because we chose a coordinate system with the positive y-axis pointing down, we must be sure to include the negative sign on all y-positions when finding heights (which must necessarily increase when moving upward).

where y_a denotes the (constant) vertical position of the center of mass of the pulley. Substituting using the relationship:

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ \omega_

Unknown macro: {p}

R = v_

Unknown macro: {b}

]\end

gives

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ m_

Unknown macro: {b}

g y_

= \frac

Unknown macro: {1}

Unknown macro: {2}

m_

Unknown macro: {b}

v_

^

+ \frac

Unknown macro: {2}

I_

Unknown macro: {p}

\left(\frac{v_{b}}

Unknown macro: {R}

\right)^

]\end

We can now solve for v_b (selecting the positive root since we are finding a speed):

Unknown macro: {latex}

\begin

Unknown macro: {large}

[ v_

Unknown macro: {b}

= \sqrt{\frac{2 g y_{b}}{1 + \frac{\displaystyle I_{p}}{\displaystyle m_

R^{2}}}} = \mbox

Unknown macro: {7.5 m/s}

] \end

The same answer as was found using method 1.

Error rendering macro 'deck'

java.lang.NullPointerException

Error rendering macro 'deck'

java.lang.NullPointerException

Unknown macro: {table}

Unknown macro: {tr}

Unknown macro: {td}

[Examples from Rotation]

Unknown macro: {tr}

Unknown macro: {td}

The root page Examples from Rotation could not be found in space Modeling Applied to Problem Solving.

Unknown macro: {search-box}

Child pages

Down the Well

Part A

Solution

Part B

Solution

Method 1

Method 2