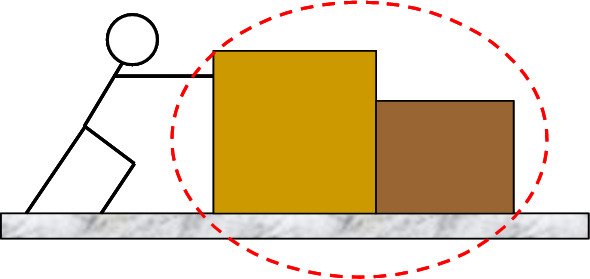
A person pushes a box of mass 15 kg along a smooth floor by applying a perfectly horizontal force F. In the process, the 15 kg box pushes against another box with a mass of 10 kg and causes it to move. The boxes accelerate horizontally at a rate of 2.0 m/s2.

    Part A

    What is the magnitude of F?

    Solution

    System:

    Both boxes together as a single point particle.

    Interactions:

    External influences from the person (applied force) the earth (gravity) and the floor (normal force).

    Model:

    Point Particle Dynamics.

    Approach:

    Part B

    What is the force applied on the front (10 kg) box by the rear (15 kg) box?

    Solution

    System:

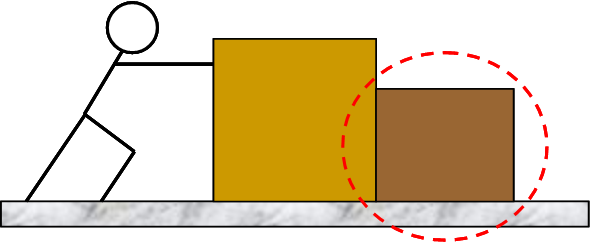
    This time, we will focus only on the front box, which will be treated as a point particle.

    Interactions:

    The front box is subject to external influences from the rear box, the earth (gravity) and the floor (normal force).

    Model:

    Point Particle Dynamics

    Approach:

    Part C

    Suppose we now consider the rear (15 kg) box as an independent system. How can we reconcile the fact that the force applied by the person to this box is 50 N, but the 15 kg box only accelerates at a rate of 2 m/s2?

    Solution

    System:

    The 15 kg box as a point particle.

    Interactions:

    The rear box is subject to external influences from the person, the rear box, the earth (gravity) and the floor (normal force).

    Model:

    Point Particle Dynamics.

    Approach: