You are viewing an old version of this page. View the current version.

Compare with Current View Page History

« Previous Version 59 Current »

Introduction to the Model

Description and Assumptions

This model applies to a rigid body which is executing pure rotation confined to the xy plane about the origin.

Learning Objectives

Students will be assumed to understand this model who can:

  • Describe what it means for a system to execute pure rotation.
  • Convert from tangential (linear) quantities to the corresponding angular quantities using the radius of the motion.
  • Explain the dependence of angular quantities and of tangential quantities describing the motion of a point on the radius of the point from the axis of rotation.
  • Define tangential and centripetal acceleration for an object in rotational motion.
  • Relate centripetal acceleration to angular velocity.
  • Give an expression for the total acceleration of any point in a rigid body executing rotational motion in terms of the angular acceleration of the body, the angular velocity of the body and the radius of the point from the axis of rotation.
  • Summarize the analogies between angular motion with constant angular acceleration and linear motion with constant (linear) acceleration.
Relevant Definitions
Relationship between Angular and Tangential Quantities
Centripetal Acceleration
Magnitude of Total Acceleration

By definition, every point in an object undergoing pure rotation will have the same value for all angular quantities (θ, ω, α). The linear quantities (r, v, a), however, will vary with position in the object.

S.I.M. Structure of the Model

Compatible Systems

This model applied to a single rigid body or to a single point particle constrained to move in a circular path.

Relevant Interactions

The system will be subject to a position-dependent centripetal acceleration, and may also be subject to an angular (or equivalently, tangential) acceleration.

Laws of Change

Mathematical Representation
Differential Form
Integral Form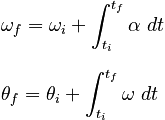

Note the analogy between these Laws of Change and those of the One-Dimensional Motion (General) model. Thus, for the case of constant angular acceleration, the integral form of these Laws are equivalent to:

Diagrammatic Representations
  • Angular position versus time graph.
  • Angular velocity versus time graph.

Relevant Examples

All Examples Using the Model
  • No labels