Introduction to the ModelDescription and AssumptionsThis model is applicable to a single point particle moving in one dimension either because it is physically constrained to move that way or because only one Cartesian component is considered. The force, or component of force along this direction, must be constant in time. The force can be in the same direction of motion or in the opposite direction of motion. Equivalently, the model applies to objects moving in one-dimension which have a position versus time graph that is parabolic and a velocity versus time graph that is linear. It is a subclass of the One-Dimensional Motion (General) model defined by the constraint da/dt = 0 (i.e. a(t)=constant). Multi-dimensional motion can often be broken into components, as in the case of projectile motion. In this manner, the 1-D motion with constant acceleration model can be employed to describe the system's motion in any situation where the net force on the system is constant, even if the motion is multi-dimensional. Learning ObjectivesStudents will be assumed to understand this model who can:
S.I.M. Structure of the ModelCompatible SystemsA single point particle, or a system such as a single rigid body or a grouping of many bodies that is treated as a point particle with position specified by the system's center of mass. Relevant InteractionsSome constant net external force must be present to cause motion with a constant acceleration. Laws of ChangeMathematical RepresentationsThis model has several mathematical realizations that involve different combinations of the variables for position, velocity, and acceleration.

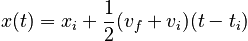

In the above expressions, ti is the initial time, the time as which the position and velocity equal xi and vi respectively. Often tiis taken to equal 0, in which case these expressions simplify. 
This is an important expression, because time is eliminated. Diagrammatic Representations
Relevant ExamplesExamples Involving Purely One-Dimensional MotionExamples Involving FreefallExamples Involving Determining when Two Objects MeetAll Examples Using this Model |
|
<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>



