|
MIT 8.01 Lesson 13: MomentumLesson SummaryThe Momentum and External Force model is introduced. This model has great utility for describing multi-body processes that occur over a finite time interval, particularly nearly-instantaneous collisions. Learning ObjectivesBy the end of this Lesson, you should be able to:
Definition and Law of ChangeAlthough Newton is famous for the law F = ma, he actually stated his Second Law in terms of momentum and its change due to impressed forces or impulses (the time integral of the force). He defined Momentum as
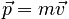
Newton's Second Law can be written in terms of momentum, and represents the fundamental law of change for the Momentum and External Force model: 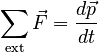
This form is totally equivalent to F = ma, provided that the system under consideration has constant mass. Unlike the traditional F = ma formulation, however, the formulation of Newton's Second Law in terms of momentum is accurate even for systems whose mass is variable. The Integral Form of Newton's Second Law and ImpulseThe Law of Change for the Momentum and External Force model can in principle be integrated: 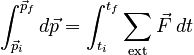
The left hand side of this expression is simple, and after some rearrangement, the equation becomes: 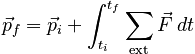
In principle, it might be useful to leave the integral over force explicit in this equation, but in practice it is not useful. If a known force which is an easily integrable function of time is applied, then it is usually just as simple and more intuitive to use the traditional F = ma approach (followed by regular kinematics). The utility of this equation actually lies in the reverse approach: using what is known about momentum to learn about the force. To facilitate this, we define the impulse associated with a force as: 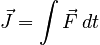
With this definition, the integral form of the Law of Change can be written: 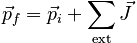
Off the Wall (Simple problem illustrating the definition of impulse and the utility of an initial-state final-state diagram.) Impulse and Time-Averaged ForceImpulse and force are closely related. In fact, if a time interval of interest is specified, the impulse imparted by a specific force during that interval can be used to quickly estimate the time-average of that force. The mathematical definition of the time-average of a force is: 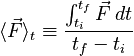
Using the definition of impulse, this expression can be written: 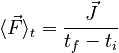
Watch Your Head (Consider the impulse and average force delivered to the head of a player performing a "header" in soccer. ) Multi-Object SystemsThe linear form of Newton's Second Law when written in terms of momentum implies that it is easily generalized to allow for a system consisting of many objects. Simply add the contributions from all the objects within the system: 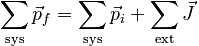
It is important to realize that although we are now allowing multiple objects within the system, the relevant impulse to add on the right hand side of Newton's Second Law is still only the external impulse. Impulses applied to one system constituent by another system constituent end up canceling out of the equation by Newton's Third Law. It is also worth noting that technically the concept of linear momentum applies only to collections of point particles. The momentum of a rigid body, then, must technically be thought of as the sum of the momentum of each of the atoms in the body. This sum turns out to be the body's mass times its center of mass velocity. The momentum of a system composed of many rigid bodies and point particles is then the sum of their individual momenta, which again can be expressed as the total mass of this system times the velocity of the system's center of mass. Conservation of MomentumOne important feature related to the fact that the Momentum and External Force model can accomodate a system composed of several constituents is the fact that, in the absence of external impulse acting on such a system, the momentum will be nontrivially conserved. For a multi-object system experiencing no net impulse, the Law of Change for the model becomes: 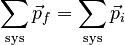
which says that the system's total momentum is conserved, but does not necessarily mean that the momentum of each constituent is conserved (this is the "nontrivial" part). Approximate Conservation in CollisionsOne of the most important types of problem involving a multi-object system is a collision problem. A collision between rigid objects is a very rapid process. Because the time of a collision is so short, and because the definition of impulse involves a time integral, everyday forces like gravity or friction usually contribute a negligible impulse during the collision. Thus, if a system is chosen that includes all the colliding objects so that the (often very large) collision forces are purposely made internal, the net external impulse during the collision will be approximately zero. This allows the use of conservation of momentum to analyze the collision. Head-on Collision (Compare the forces on the occupants of two cars in a 1-D totally inelastic collision.) Out of Bounds (A typical perfectly inelastic collision in 2-D.) A Walk on the Pond (How far will two children slide after a perfectly inelastic collision? ) |
|||||||||||||||||||||
Overview
Content Tools
Activity




