|
Introduction to the ModelDescription and Assumptions1-D Angular Momentum and Torque is a subclass of the general Angular Momentum and External Torque model in which a system of rigid bodies is constrained to move only in a plane (usually taken to be the xy plane) with each body's angular momentum therefore directed along an axis perpendicular to the plane (along the z-axis). Under these conditions, the angular momentum is a one-dimensional vector, and the directional subscript (z) is generally omitted. Learning ObjectivesStudents are assumed to understand this model who can:
Relevant DefinitionsAngular momentum about axis a: 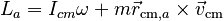
S.I.M. Structure of the ModelCompatible SystemsThe system can be composed of any number of rigid bodies and point particles. The system must either be constrained to move in such a way that the angular momentum will be one-dimensional, or else the symmetries of the situation (system plus interactions) must guarantee that the angular momentum will remain one dimensional. Relevant InteractionsExternal interactions must be explicitly given as torques, or as forces with their point of application or moment arm about a chosen axis of rotation specified along with their magnitude and direction. (Internal interactions do not change the angular momentum of the system.) Laws of ChangeMathematical RepresentationDifferential Form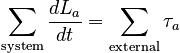 Integral Form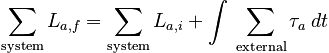
where the last term is called the "angular impulse" Diagrammatic RepresentationsRelevant ExamplesExamples Involving Constant Angular MomentumExamples Involving Rolling without SlippingExamples Involving the Parallel Axis TheoremAll Examples Using this Model
|
|
<script type="text/javascript">
var gaJsHost = (("https:" == document.location.protocol) ? "https://ssl." : "http://www.");
document.write(unescape("%3Cscript src='" + gaJsHost + "google-analytics.com/ga.js' type='text/javascript'%3E%3C/script%3E"));
</script>
<script type="text/javascript">
try {
var pageTracker = _gat._getTracker("UA-11762009-2");
pageTracker._trackPageview();
} catch(err) {}</script>

